• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Приклад 2 2 страница

Розглянемо вплив періоду функції f(t) на вигляд спектральної діаграми. Для цього представимо f(t) у формі, поданій на Рис. 10.12

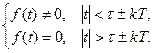
Таке подання відповідає імпульсному коливанню, тобто коливанню, що містить часові ділянки, протягом яких f(t) має незмінні значення, наприклад, нульові. Від періоду Т залежить відстань на осі частот між сусідніми лініями спектра.

тобто, із збільшенням періоду спектр густішає. У той же час амплітуда кожної гармоніки

зменшується. Якщо скористатися заміною 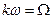, тобто розглядати неперервну зміну частоти, можна одержати вираз для обвідної спектра, тобто неперервної кривої, що на частотах гармонік має значення їх амплітуд. Ця крива називається спектральною функцією

. (10.27)

Відвідповідно,

.

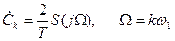На Рис. 10.13 подано спектральну функцію імпульсного коливання та два дискретних спектри, що відповідають періодичним послідовностям імпульсних коливань однакової форми, період яких відрізняється вдвічі. Як видно з рисунку, різниця між спектрами полягає у подвоєнні кількості гармонік на смугу частот, та зменшенні удвоє амплітуд гармонік.

У загальному випадку гармоніки мають дійсну та уявну складові. Але, якщо 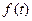є парною функцією, тобто 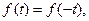тоді

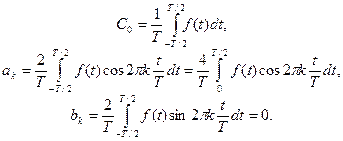(10.28)

і ряд Фур’є буде містити тільки косинусні складові

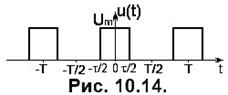
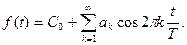(10.29)

Наприклад, парну періодичну послідовність прямокутних імпульсів, вид якої подано на Рис. 10.14 можна описати виразом

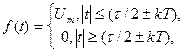(10.30)

де 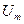- амплітуда імпульсів, 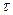- тривалість, - період повторення імпульсів.

Підставимо функцію (30) у формули (28) і одержимо величини спектральних складових

(10.31)

У формулах (31) введено параметр 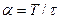, який називається шпаруватістю.

На Рис. 10.15 побудовані лінійчаті спектри періодичної послідовності прямокутних імпульсів (30), розраховані за формулами (31) для двох значень шпаруватості, за умови, що змінюється тривалість імпульсів, а період послідовності залишається незмінним.

У разі непарної функції, тобто коли коефіцієнти Фур’є дорівнюють

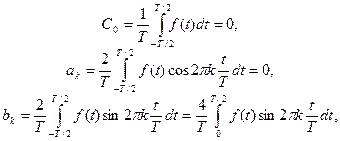(10.32)

і ряд Фур’є буде містити тільки синусні складові

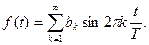(10.33)

Наприклад, пилкоподібна функція (див. Рис.10.16) може бути подана виразом

(10.34)

Підставляючи цей вираз у формули (32) для визначення амплітуд гармонік, одержимо

Після підставлення одержаного виразу у розкладення (33), одержимо лінійчатий спектр непарної пилкоподібної функції

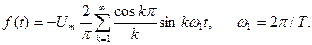(10.35)

Спектральну діаграму, побудовану за формулою (35) подано на Рис. 10.17.

10.5. Потужність та дієве значення періодичного коливання

Під час аналізу енергетичних співвідношень у радіоелектронних колах розглядають миттєву активну потужність, що споживається опором величиною 1 Ом, тобто вважають, що 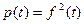. Середня потужність періодичного коливання у цьому випадку дорівнює

(10.36)

Підставимо у вираз (36) розкладення Фур’є функції f(t) з (23)

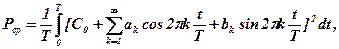
Інтегруючи вираз з урахуванням умови ортогональності, одержимо

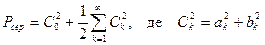(10.37)

Тобто, середня потужність періодичного коливання дорівнює сумі середніх потужностей його гармонічних складових. Дієве значення f(t) (u_d абоi_d )

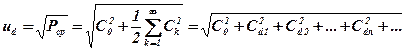, (10.38)

бо для синусоїд

Співвідношення 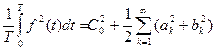(10.39)

називається рівністю Парсеваля для періодичного коливання і подає розподіл потужності коливання f(t) по частотах його гармонік.

10.6. Перетворення Фур’є неперіодичного коливання

Розклад Фур’є може бути узагальнений і на випадок неперіодичної функції. Неперіодичну функцію можна розглядати як крайній випадок періодичної за умови, що її період нескінченно збільшується, тобто . Візьмемо ряд Фур’є у комплексній формі

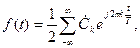
і підставимо у нього комплексні амплітуди гармонік

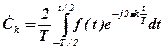
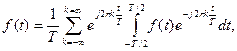(10.40)

Визначимо, як і раніше, та виконаємо граничні переходи

де - поточна частота, що змінюється неперервно, - приріст поточної частоти .

За наведених умов сума у виразі (40) перейде у інтеграл

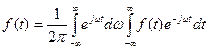(10.41)

або (10.42)

де (10.43)

Вираз (43) називається прямим, а вираз (42) – оберненим перетворенням Фур’є. Загалом, вирази (43) та (42) подають пару перетворень Фур’є, які зв’язують між собою дійсну функцію часу f(t) та комплексну функцію частоти . Зміст виразу (42) полягає в тому, що неперіодична функція f(t) подається сумою періодичних синусоїдних коливань. Таке подання можливе тільки за умови підсумовування нескінченно великої кількості нескінченно малих синусоїдних коливань з нескінченно близькими частотами. Тобто, спектр неперіодичної функції f(t) є суцільним (неперервним). Комплексна амплітуда кожної нескінченно малої складової дорівнює

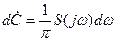, (10.44)

частотний інтервал між складовими - 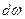. Відношення цих нескінченно малих утворює скінчену величину

, (10.45)

яка називається спектральною густиною функції f(t).

Таким чином, ми маємо два види спектрів коливань: лінійчаті та суцільні. Гармонічні лінійчаті спектри відповідають періодичним коливанням, суцільні – неперіодичним.

10.7. Основні властивості спектрів коливань

1. Перетворення Фур’є є лінійним і підлягає принципу суперпозиції, тобто спектр суми коливань дорівнює сумі їх спектрів

(10.46)

2. Якщо часовій функції 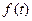відповідає спектр , то спектр коливання, зсунутого у часі, дорівнює

Використаємо у інтегралі нову змінну 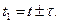У підсумку одержимо

, (10.47)

тобто, під час зсуву функції у часі, форма її спектральної функції залишається незмінною, а кожна спектральна складова набуває зсуву фази на величину 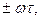залежну від частоти складової. Іншими словами форма амплітудного спектра не залежить від вибору початку відліку часу.

3. Спектр коливання, зсунутого вздовж осі частот

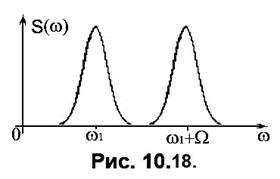На Рис. 10.18 подано дві спектральні функції однакової форми, але зосереджені навколо різних середніх частот та . Якщо спектру відповідає функція часу 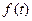, то якій функції часу відповідає спектр

У загальному випадку

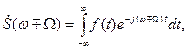
звідки

відповідно, часова функція під час зсуву спектра за частотою набуває множника 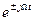, тобто домножується на гармонічну функцію, частота якої дорівнює різниці середніх частот спектрів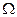

(10.48)

З виразу (48) витікає спосіб частотного ущільнення інформаційних каналів, який полягає у тому, що для одночасного передавання повідомлень, спектри яких найчастіше знаходяться у одному діапазоні частот (мовлення, телебачення), часову функцію, яка відтворює повідомлення, слід домножати на гармонічні функції різних частот 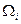. Єдина вимога під час ущільнення каналів полягає у запобіганні перекриттю за частотою спектрів різних повідомлень, тобто

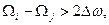
де 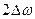- смуга частот, відведена для передавання кожного повідомлення.

4. Спектр коливання із зміненим масштабом часу

Якщо функція 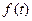має спектр, то зміна масштабу часу, тобто виконання операції 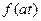, перетворює спектр таким чином

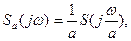(10.49)

тобто зміна тривалості коливання не змінює форму спектра, а змінює його ширину – коротшому імпульсу відповідає ширший спектр і навпаки. Розглянемо, наприклад, спектр 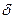-імпульсу, який має найкоротшу тривалість . Підставимо 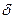- імпульс у формулу перетворення Фур’є

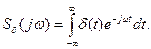
Спираючись на фільтрувальну властивість 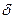- імпульсу (див. вираз (10.20)), маємо

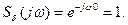
Тобто спектр найкоротшого імпульсу має нескінченну ширину, іншими словами, має стале значення спектральної густини на будь-якій частоті.

5. Спектр диференційованого у часі коливання

Виходячи з того, що спектр є нескінченою сумою комплексних експоненційних функцій 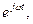і згадуючи, що 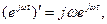одержимо наступну властивість спектра. Якщо функція 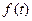має спектр , то спектр диференційованої за часом функції

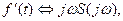(10.50)

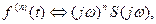(10.51)

де символом позначатимемо пряме та обернене перетворення Фур’є. Таким чином, операції диференціювання функції у часовій області відповідає множення її спектра на лінійно залежний від частоти множник .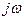

6. Спектр інтегрованого коливання.

Згадуючи положення, наведене у попередньому пункті, та те, що 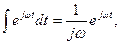маємо: якщо , то

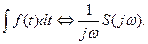(10.52)

Таким чином, операції інтегрування функції у часовій області відповідає ділення її спектра на лінійно залежний від частоти дільник .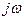

7. Множення коливань та спектрів.

Згорткою двох функцій часу називається співвідношення між ними наступного виду

. (10.53)

Визначимо спектр коливання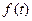

.

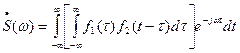Змінюючи порядок інтегрування і враховуючи співвідношення (47) щодо спектра зсунутого за часом коливання, одержимо

(10.54)

Таким чином, спектр згортки двох коливань дорівнює добутку їхніх спектрів.

Внаслідок взаємної оберненості частоти і часу, спектр коливання, що є добутком двох коливань

,

повинен являти собою згортку їхніх спектрів, тобто

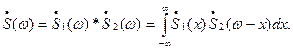(10.55)

8. Енергія коливання дорівнює

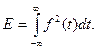
Цей інтеграл є скінченим, наприклад, для коливань, обмежених за часом. Для коливань, що не дорівнюють нулю на нескінченності, інтеграл розбігається. Тому для таких коливань визначають не енергію, а потужність, що дорівнює енергії за одиницю часу.

Використовуючи пару перетворень Фур’є (42) та (43), енергію коливання можна подати у вигляді

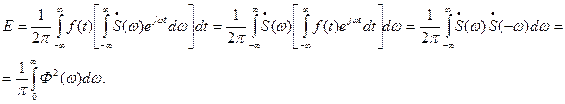
Таким чином

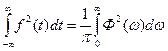, (10.56)

де - спектральна потужність енергії або енергетичнийспектр коливання. Співвідношення (56) називається рівністю Парсеваля для неперіодичних коливань. Енергетичний спектр показує розподіл енергії коливання за частотою, але не містить інформації про фазу коливання і тому за енергетичним спектром не можна відновити форму коливання. Наприклад, на Рис. 10.19 наведено спектральні і часові діаграми двох коливань, що мають однаковий енергетичний спектр. Обидва є сумою двох гармонік, але відмінність між ними полягає у різниці фаз другої гармоніки, що дорівнює 180⁰. Як видно, коливання відрізняються за формою.

9. Інтеграл збігається тільки за умови абсолютної збіжності функції f(t), тобто за умови

, (10.57)

що завжди виконується для реальних коливань, бо ця умова тотожна умові скінченності енергії коливання. Але, під час розгляду ідеальних моделей, виконання цієї умови необхідно обговорювати у кожному конкретному випадку. Наприклад, одиничний стрибок 1(t) не відповідає умові (10.57), бо .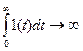

10.8. Спектральні характеристики моделей коливань

Знайдемо спектр 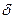-функції, скориставшись її фільтрувальною властивістю (20)

(10.58)

Якщо 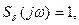тобто спектр 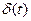має однакове значення на усіх частотах, яке дорівнює одиниці. Виходячи з лінійності перетворення Фур’є (46) та виразу (58), спектр напівсуми двох 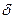-функцій

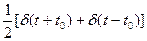
дорівнює

Виконуючи обернене перетворення Фур’є над виразом (58), маємо

це, до речі, ще один запис 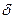-функції. Тобто, якщо косинусоїдне коливання подається у вигляді

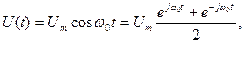
його спектр має вигляд

(10.59)

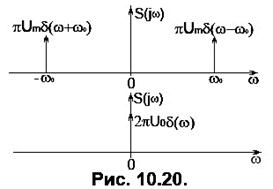
Таким чином, спектр косинусоїдного коливання є парою -функцій на осі частот, площа яких пропорційна амплітуді косинусоїди. Відповідно, спектр сталої напруги, тобто косинусоїди з періодом дорівнює

(10.60)

і є єдиною -функцією на початку осі частот. Спектри косинусоїди та сталої напруги подано на Рис. 10.20.

Визначимо далі спектр одиничного стрибка, для якого не виконується умова абсолютної збіжності, бо 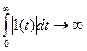. Щоб задовольнити цю умову, домножимо стрибок на множник збіжності . У підсумку маємо функцію , де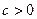(див. Рис. 10.21). Визначимо спектр цієї функції, виконуючи пряме перетворення Фур’є:

(10.61)

Формула (61) подає спектр експоненційного імпульсу, що розташований у точці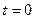

(10.62)

Спрямовуючи с до нуля, одержимо спектр одиничного стрибка

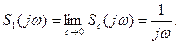(10.63)

10.9. Обчислення спектрів імпульсних коливань

Спектральні густини імпульсів можна розраховувати, підставляючи функції, що описують імпульси, у формулу прямого перетворення Фур’є (43) і виконуючи інтегрування в межах існування імпульсу. Визначимо, наприклад, у такий спосіб спектр парного прямокутного імпульсу

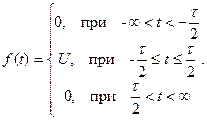
(10.64)

де 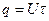- площа імпульсу. Розмірність спектральної густини Вс або В/Гц.

Для побудови спектра проаналізуємо хід функції (64) із зміною частоти. Для визначення спектра на частоті 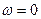слід розкрити невизначеність виду 0/0. Скористаємося правилом Лопіталя 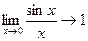, звідки тобто спектр на частоті дорівнює площі імпульсу. Ця властивість є загальною для спектральної густини імпульсу будь-якої форми, тому що

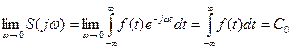, (10.65)

а це - стала складова, частота якої саме дорівнює нулю. Чисельник функції (64) є знакозмінною функцією, а це означає, що половина складових спектра, які є синусоїдами різних частот, має від’ємне значення. Тобто фази цих синусоїд відрізняються на 180⁰. Визначимо точки зміни знаків чисельника, а саме частот, на яких відбуваються стрибки фази складових спектра: , якщо .Таким чином, положення нулів спектральної густини залежить від тривалості імпульсу 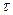. Обвідна спектра, тобто крива, за межі якої функція не виходить за будь-яких умов, визначається знаменником виразу (64). Це – гіпербола, яка прямує до нуля, якщо . Ця обставина ще раз підкреслює збіжність інтегралу Фур’є за умови скінченності енергії коливання – у нашому випадку 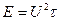. Враховуючи всі наведені обставини, можемо зобразити графік спектра прямокутного імпульсу на Рис. 10.22. Розглянутий імпульс є парною функцією, відповідно, спектр його також буде парною функцією. Крім того, всі складові спектра мають фази або 0, або 180⁰, тому цю комплексну функцію можна зобразити на одному графіку. У загальному випадку слід подавати модуль і фазу комплексного спектра. На Рис. 10.22 подано спектр у діапазоні частот . Такий спектр називається математичним. Частіше розглядають фізичний спектр, утворений підсумовуванням складових з реальними додатними частотами. Зв’язок між математичним та фізичним спектрами дають співвідношення .

(10.66)

Визначимо спектр прямокутного імпульсу загального виду, наприклад, такого, що починається у точці , подавши його як різницю двох зсунутих у часі стрибків амплітудою U

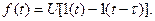
Скориставшись першою та другою властивостями спектрів (див. розд. 10.7), а також виразом (63) для спектра одиничного стрибка, маємо

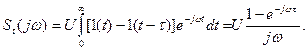(10.67)

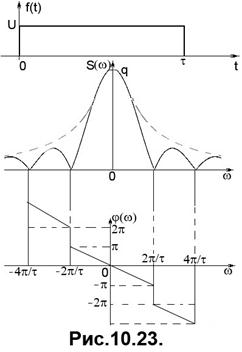
З виразу (67) видно, що спектр – комплексний. Приведемо його до форми, подібної попередньому прикладу парного імпульсу

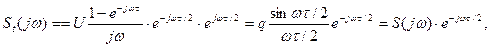(10.68)

тобто підтвердимо другу властивість спектра щодо зсуву функції у часі. Форма спектра залишилася незмінною (див. Рис. 10.23), а до фазової характеристики додається лінійна функція частоти

Енергетичний спектр імпульсу є дійсним

(10.69)

і незалежним від часового положення імпульсу.

Під час розрахунку спектрів імпульсних коливань часто зручно використовувати не пряме перетворення Фур’є, а наведені вище властивості спектрів, зокрема положення про спектр похідної від функції. При цьому слід пам’ятати, що похідна від розривної функції у точці розриву дорівнює 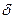-функції, площа якої дорівнює величині стрибка функції.

Визначимо спектри імпульсів різної форми у такий спосіб. У якості контрольного прикладу знову розрахуємо спектр парного прямокутного імпульсу, зображеного на Рис. 10.24. Похідна цього імпульсу описується виразом

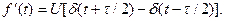
Спектр похідної дорівнює різниці спектрів двох зсунутих у часі 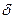-імпульсів

З іншого боку, спектр похідної дорівнює

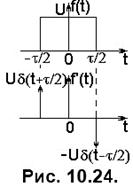
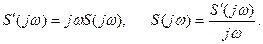
Підставимо спектр похідної прямокутного імпульсу у останній вираз

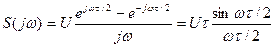(10.70)

і одержимо вже відомий вираз спектра парного прямокутного імпульсу. Таким же чином розрахуємо спектри імпульсів поширених форм.

На Рис. 10.25 подано парний трикутний імпульс та дві його похідні за часом. Функція, що описує імпульс має вигляд

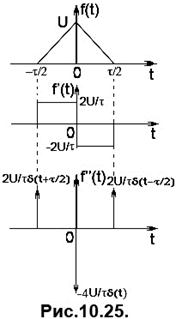
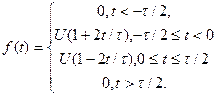
Перша похідна описується виразом

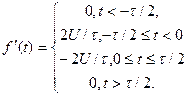
Друга похідна

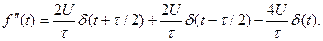
Спектр цієї часової функції має вигляд

Читайте також:

1. I. ОБРАЗОВАНИЕ СОЕДИНЕННЫХ ШТАТОВ 14 страница
2. А. В. Дудник 1 страница
3. А. В. Дудник 10 страница
4. А. В. Дудник 11 страница
5. А. В. Дудник 12 страница
6. А. В. Дудник 2 страница
7. А. В. Дудник 3 страница
8. А. В. Дудник 4 страница
9. А. В. Дудник 5 страница
10. А. В. Дудник 6 страница
11. А. В. Дудник 7 страница
12. А. В. Дудник 8 страница

Переглядів: 926