• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Приклад 2 3 страница

З іншого боку, спектр другої похідної дорівнює

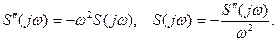
Підставивши спектр другої похідної у останній вираз, одержимо спектр парного трикутного імпульсу

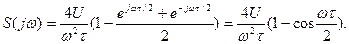
Після нескладних перетворень остаточно одержимо

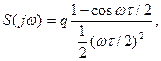(10.71)

де - площа імпульсу. Фізичний спектр цього імпульсу, побудований за виразом (71), подано на Рис. 10.26. Як видно з виразу (71), усі спектральні складові є дійсними величинами, тобто фаза складових на усіх частотах дорівнює нулю. Пунктиром на рисунку подано обвідну спектра, що є квадратичною параболою.

На Рис. 10.27 подано зображення косинусоїдного імпульсу та перших двох похідних за часом. Функція, що описує цей імпульс має вигляд

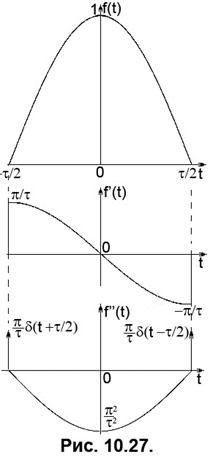
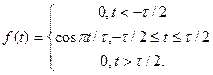
Її перша похідна дорівнює

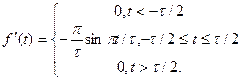
Друга похідна у межах існування імпульсу

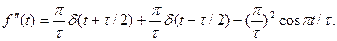
Скориставшись визначенням спектра другої похідної, маємо

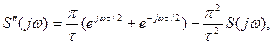
де останній член у сумі є поки невідомим спектром імпульсу. З іншого боку

тобто

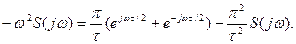
Розв’язуючи отримане рівняння відносно невідомого , одержимо шуканий спектр парного косинусоїдного імпульсу.

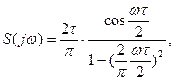(10.72)

де 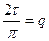- площа косинусоїдного імпульсу. Обвідна спектра також є квадратичною параболою. На частоті має місце невизначеність виду , яка розкривається за допомогою правила Лопіталя

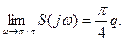
Спектральна функція перетинає вісь частот у точках 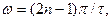де

10.10. Зв’язок між часовими та спектральними характеристиками коливань

Співставляючи коливання та їхні спектри, можна встановити ряд закономірностей:

- скінченому за часом (фінітному) коливанню відповідає нескінченний спектр (приклад – прямокутний імпульс), а скінченому за частотою спектру відповідає нескінченне за часом коливання(приклад – синусоїда, або стала напруга);

- спектри більшості імпульсів мають хвилеподібну форму з нульовими значеннями у окремих точках частотної осі. Це пояснюється тим, що найчастіше імпульси утворені сукупністю однакових за формою та величиною елементів, зсунутих у часі. Спектр такої сукупності є результатом інтерференції спектрів цих елементів, що відрізняються тільки фазами складових. У підсумку на деяких частотах можлива їх точна компенсація і утворення нулів сумарного спектра;

- хвилеподібні спектри імпульсів мають обвідні, які є спадними функціями. Швидкість згасання обвідних залежить від наявності розривів (стрибків) у функції, що описує імпульс, або її похідних. Наприклад, обвідна спектра прямокутного імпульсу (який є різницею стрибків) - пропорційна 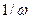, а обвідні спектрів трикутного та косинусного імпульсів, які мають розриви перших похідних, є пропорційними ;

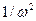- теоретична нескінченність спектра імпульсів потребує уточнення щодо смуги зайнятих частот, коли мова йде про параметри конкретної системи передавання інформації.

На практиці під шириною спектра коливання зазвичай розуміють смугу частот, у якій зосереджено переважну частину енергії коливання. Для приблизних оцінок у техніці вважають, що

або 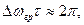(10.73)

де 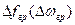- ширина спектра, відрахована на визначеному рівні спектральної густини, або між характерними точками спектра, 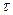- тривалість коливання, відрахована на визначеному рівні. Застосування умови (73) до прямокутного імпульсу дає

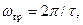(10.74)

тобто, за ширину спектра прямокутного імпульсу вважається ширина першої пелюстки його спектра. У цій смузі зосереджено більше 90% енергії імпульсу.

Обмеження ширини спектра коливання, ясна річ, призведе до зміни його форми. Наприклад, виконуючи обернене перетворювання Фур’є обмеженого за частотою спектра прямокутного імпульсу, одержимо різні за ступінню спотворень імпульси, що за формою наближаються до прямокутного. Якість наближення покращується із збільшенням ширини спектра, тому вибір ширини спектра у реальних системах завжди є результатом компромісу між бажаною якістю системи і шириною смуги частот, яку вона займає. На Рис. 10.28 подано необмежений за частотою спектр прямокутного імпульсу, а також два імпульси, одержані на виході ідеального фільтру нижніх частот з граничною частотою, що дорівнює, відповідно, 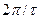та 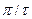. Оптимізація зайнятої смуги частот можлива лише за умови урахування шумів, що діють у каналі передавання інформації.

10.11. Шуми і завади у радіоелектронних системах

10.11.1. Джерела шумів та завад

Параметри сигналів у радіоелектронних системах завжди мають випадкові зміни, не пов’язані із змістом переданого повідомлення, спричинені такими факторами:

1. хаотичним тепловим рухом носіїв зарядів у провідниках пристроїв, який існує і без зовнішніх напруг;
2. неперервними змінами (флуктуаціями) числа електронів та дірок, що перетинають потенціальні бар’єри у напівпровідникових пристроях;
3. зміною параметрів елементів радіоелектронних пристроїв та властивостей каналів, де поширюються ЕМХ, під впливом змін навколишнього середовища (температури, вологості, тиску, іонізації атмосфери тощо);
4. неконтрольованими зовнішніми електромагнітними впливами на системи приймання інформації.

Ці випадкові струми і напруги, що з’являються у колах РЕА, негативно впливають на процеси одержання повідомлень і тому називаються завадами.

Хаотичні струми і напруги, викликані першими двома чинниками, на виході пристроїв оброблення звукової інформації сприймаються як звуковий шум. Тому завади такого типу і у інших системах також прийнято називати шумами. Рівень шумів найчастіше залежить від схеми, конструкції та характеристик елементів приймального пристрою.

Крім того, під час приймання електромагнітних коливань завжди є завади від зовнішніх джерел, а саме: розрядів блискавки, радіовипромінювань Сонця, зірок та планет, іскрових та дугових розрядів промислового та транспортного обладнання. Для споживача інформації вони також є випадковими, бо ніяким чином не пов’язані із змістом одержаного повідомлення. Також існує широкий клас організованих завад для виводу з ладу каналів передавання інформації супротивника під час озброєних зіткнень.

Виходячи з наведеного, одним з головних завдань радіоелектроніки є розроблення методів та створення засобів одержання якісної інформації за наявності шумів та завад.

10.11.2. Основні характеристики випадкових процесів як моделей шумів

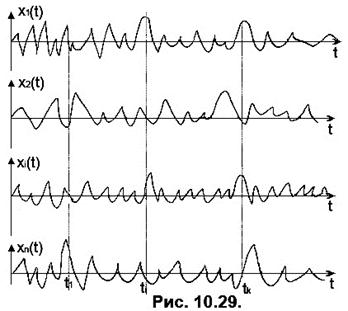
Моделлю шумового коливання у електронному колі може бути випадковій процес x(t), тобто коливання, що є функцією часу x_к(t) в умовах к-го експерименту, кожне миттєве значення якого (при t=t_i) є випадковою величиною x(t_і). Запис функції x_к(t) називається к-ю реалізацією випадкового процесу. Під час кожного наступного експерименту вид функції x_к(t) змінюється, а встановити характер її зміни заздалегідь неможливо. Сукупність реалізацій називають ансамблем реалізацій випадкового процесу. Ансамбль реалізацій випадкового процесу подано на Рис. 10.29. Випадкову величину x(t_і) називають перетином випадкового процесу, що відповідає аргументу t=t_i. На Рис. 10.29 показано три перетини процесу у точках 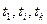. Для аналізу такої моделі слід застосувати апарат теорії ймовірності.

Всі миттєві значення випадкового процесу можна розділити на дві групи – можливі та неможливі. Неможливі – це значення, які не можна одержати ні у одному з експериментів. Кількісною мірою можливості того чи іншого значення випадкового процесу є ймовірність появи цього значення. Всі реальні експерименти можна описати двома моделями - неперервною (аналоговою) та дискретною. Аналогова модель – описує записи мовлення, музики тощо, тобто у межах аналогової моделі коливання приймає будь-яке миттєве значення у межах можливого. Дискретна модель – описує кидання монети, кубика, гральних карт, лотерею, цифрову або літерну послідовність, тобто вибір одного значення із заздалегідь відомої сукупності даних. Враховуючи призначення моделі шуму, а саме – надання можливості аналізу впливу шуму на миттєві значення прийнятого повідомлення, слід знати такі характеристики модельного випадкового процесу:

- ймовірність одержання тих, чи інших, його миттєвих значень,

- швидкість зміни його миттєвих значень,

- характер зв’язку між миттєвими значеннями у реалізації процесу.

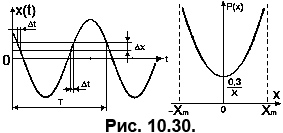Саме поняття ймовірності має різний зміст у залежності від характеру процесу, що підлягає аналізу. У разі дискретної моделі визначення ймовірності можна звести до так званої схеми випадків, тобто вважати ймовірністю того чи іншого значення процесу відношення кількості появ даного значення до всієї кількості зроблених випробувань. Наприклад, багаторазове кидання монети дає приблизно однакову кількість випадінь герба та цифри. Для опису аналогових випадкових процесів зручно користуватись визначенням ймовірності, як відношенням часу перебування процесу у заданих межах до тривалості реалізації. Наприклад, на Рис. 10.30 показано процес визначення ймовірності миттєвих значень синусоїди, як відношення часу її перебування 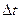у межах до періоду синусоїди. Результат розрахунку поданий на Рис.10.30 праворуч.

Ймовірність одержання тих, чи інших миттєвих значень процесу описується функцією розподілу ймовірностей миттєвих значень. Це функція, що визначає ймовірність того, що миттєве значення реалізації є меншим ніж певне число U, тобто

. (10.75)

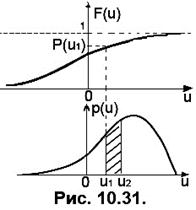
Функція може бути аналоговою або дискретною, в залежності від можливих миттєвих значень випадкового процесу. Відповідно,. Щоб знайти ймовірність знаходження миттєвих значень у заданих межах зручніше користуватись похідною від функції розподілу ймовірностей, що називається густиною розподілу ймовірностей (див. Рис. 10.31)

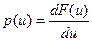. (10.76)

Тоді ймовірність знаходження миттєвих значень у межах визначається так:

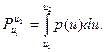(10.77)

Умова нормування густини ймовірностей

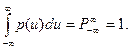(10.78)

Закони розподілу ймовірностей миттєвих значень визначаються для кожного перетину випадкового процесу і, у загальному випадку, є функціями часу. Якщо закони розподілу ймовірностей не залежать від часу, процес називається стаціонарним. Стаціонарність є зручним модельним поданням випадкового процесу, бо, у реальних умовах, хід процесів завжди змінюється з плином часу. Якщо ж розглядати процеси, що відбуваються за незмінних умов (сталість температури, тиску тощо), така модель є продуктивною для аналізу. Використання умови стаціонарності дозволяє визначати закони розподілу ймовірностей за однією реалізацією процесу, не вдаючись до ансамблю реалізацій.

У техніці користуються окремими параметрами закону розподілу, що називаються моментами розподілу. Найчастіше використовуються:

- математичне сподівання або середнє значення:

для аналогових процесів

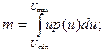(10.79)

де 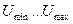- область існування випадкового процесу.

Для дискретних процесів

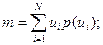(10.80)

у випадку стаціонарного процесу

(10.81)

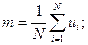(10.82)

тобто матсподівання стаціонарного процесу дорівнює сталій складовій реалізації випадкової напруги тривалістю .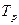

- дисперсія, що описує розкид миттєвих значень процесу відносно матсподівання:

для аналогових процесів

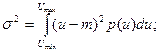(10.83)

для дискретних процесів

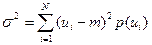. (10.84)

За умови стаціонарності процесу

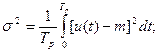(10.85)

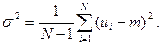(10.86)

Величину називають середньоквадратичним відхиленням. Якщо m = 0, тобто відсутня стала складова, процес називається центрованим і дисперсія дорівнює енергії змінної складової процесу.

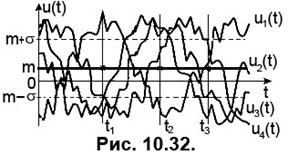На Рис. 10.32 наведено чотири реалізації випадкового процесу, показані на одному графіку. У трьох точках часової осі зроблено перетини, у яких розраховано матсподівання та дисперсію. Розраховані у перетинах значення виявилися сталими, тобто показаний на рисунку процес є стаціонарним.

Вид функцій залежить від фізичних властивостей процесу, що моделюється, та наявних відомостей про нього. Коли відомі тільки межі, у яких можуть знаходитись миттєві значення, користуються моделлю, що має рівномірний закон розподілу (Рис. 10.33,а), тобто

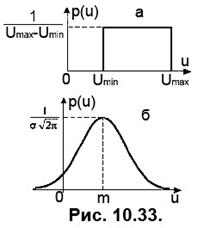
Переважна більшість процесів, що відбуваються у природі, є результатом дії багатьох незалежних чинників, тому закон розподілу миттєвих значень таких процесів у відповідності з центральною теоремою теорії ймовірностей є нормальним (Рис. 10.33,б), тобто

де Ф(u-m) –таблична функція інтеграл ймовірності. Ось деякі її значення

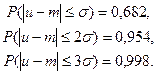
Для визначення швидкості зміни миттєвих значень випадкового процесу використовується автокореляційна функція

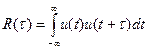, (10.87)

яка подає степінь зв’язку між реалізаціями процесу, зсунутими у часі. При 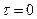для центрованого процесу, виходячи з виразу (85), 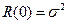. Розділивши вираз (87) на 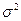, одержимо нормований параметр процесу, який називається коефіцієнтом кореляції

. (10.88)

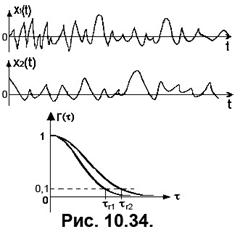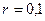Для оцінювання власне швидкості зміни процесів вводять інтервал кореляції – часовий зсув , при якому коефіцієнт кореляції зменшується до заданого рівня , тобто . Зазвичай обирають . Іноді за інтервал кореляції приймають основу прямокутника, що має амплітуду, що дорівнює одиниці, площа якого є рівною площі під функцією 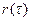. Процеси, що змінюються повільно, мають більший інтервал кореляції і навпаки. На рис. 10.34 подані дві реалізації випадкових процесів, які відрізняються швидкістю зміни миттєвих значень. Відповідно, другий процес має більший інтервал кореляції у наведеному сенсі.

Найшвидшим випадковим процесом є електронний струм у провіднику, який кожної миті є сумою незчисленної кількості електронів, проходження кожного з яких можна вважати дельта-імпульсом струму. Такий шум вважають дельта-корельованим, тобто таким, інтервал кореляції якого прямує до нуля. Враховуючи, що спектр дельта-імпульсу є рівномірним на усій частотній осі, по аналогії з білим світлом, що складається з багатьох кольорів, такий шум називають «білим шумом».

Логічно спробувати скористатися для аналізу шумів тим же спектральним методом, що й для детермінованих коливань. Однак, безпосередньо застосовувати спектральний розклад випадкового процесу недоцільно, бо спектр кожної нової реалізації буде новою випадковою функцією. Доцільно ввести усереднену спектральну характеристику. Одержати її можна таким чином. Підставимо у вираз (87) замість зсунутого у часі коливання його спектральне подання

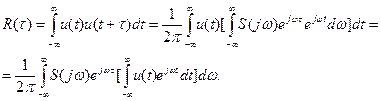
Враховуючи, що 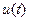є дійсним процесом, можна вважати, що комплексно спряжений процес має такий же вигляд - 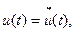звідки спектр комплексно спряженого процесу

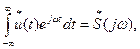
Відповідно,

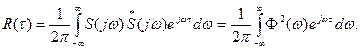(10.89)

По аналогії з перетворенням Фур’є

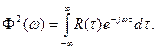(10.90)

Співвідношення (89) та (90) називаються теоремою Вінера-Хінчина і пов’язують спектральну густину потужності процесу з його автокореляційною функцією. Як видно, тут також зберігається основне співвідношення між часовими та спектральними характеристиками коливань – повільним змінам процесу, тобто протяжній у часі автокореляційній функції відповідає менший за смугою енергетичний спектр і навпаки. Співвідношення (89) та (90) дозволяють оцінювати енергетичний вплив шумів на різні ділянки спектра сигналу, але нічого не кажуть про спотворення форми сигналу, бо у енергетичному спектрі втрачено інформацію про фазу, від якої залежить форма сигналу.

Білий шум, викликаний хаотичним тепловим рухом зарядів є основним чинником, який погіршує якість приймання сигналів. Джерелами цього шуму є усі без винятку елементи приймача. Шум додається до підсилюваного сигналу і вносить випадкові спотворення. Найбільший вплив мають елементи, що шумлять на вході приймача, бо їхні шуми підсилюються таким же чином, як і прийнятий слабкий сигнал. Теоретично такий шум має нескінченно велику енергію, бо розподілений у безмежній смузі частот. Реально енергія білого шуму залежить від ширини смуги прозорості приймального пристрою і визначається формулою Найквіста

(10.91)

де к = 1,37*10^-23 Втс/град - стала Больцмана; Т – абсолютна температура К⁰; R – активний опір, що є джерелом шуму; 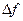- смуга прозорості приймального пристрою. Визначимо, наприклад, середньоквадратичну напругу шуму за таких умов:

.

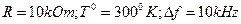
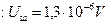Таким чином, враховуючи, що напруга шуму є на затискачах активного опору і за відсутності зовнішньої напруги, найпростішою моделлю реального активного опору є подане на Рис. 10.35 з’єднання опору з джерелом шумової напруги (або струму).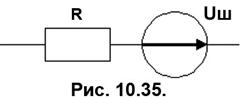

Вплив шуму на сигнал оцінюється відношенням сигнал/шум, яке найчастіше розраховується за потужністю у смузі приймача

. (10.91)

Припустиме значення відношення сигнал/шум залежить від завдань конкретного радіотехнічного пристрою. Наприклад, досвідчений оператор приймає азбуку Морзе при С/Ш<1, виявлення сигналу у радіолокації відбувається за умови С/Ш>2, чутливість радіомовного приймача визначається за умови С/Ш=10, якісне телебачення потребує С/Ш>100, у швидкісних лініях зв’язку С/Ш>1000 тощо.

Шумові властивості підсилювачів та приймачів прийнято характеризувати коефіцієнтом шуму

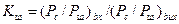, (10.92)

який показує, як погіршується відношення сигнал/шум під час оброблення сигналу пристроєм. Якщо підсилювач не шумить, 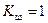. Враховуючи, що коефіцієнт підсилення потужності дорівнює , одержимо .

10.11.3. Завадостійке приймання сигналів

Приймання будь-якого сигналу можливе тільки за наявності попередніх відомостей щодо нього. Це можуть бути відомості про ті, чи інші фізичні параметри сигналу, наприклад, інтенсивность, носійну частоту, час появи, тривалість тощо.

Деякі з цих параметрів є сталими і їх слід розглядати як ознаки сигналу і найкращим чином використовувати для розрізнення сигналу і завади.

Інші параметри, що є інформаційними, можна в той, чи інший спосіб модулювати, тобто ставити в залежність від повідомлення, що слід передати. Заздалегідь відомими є лише діапазон та характер можливих змін інформаційних параметрів повідомлення.

Завдання приймання сигналів можна звести до трьох основних:

1. виявлення сигналу;
2. розрізнення сигналів;
3. відновлення повідомлення.

Під виявленням сигналу слід розуміти відповідь на питання: чи є на вході приймача суміш сигналу з шумом, чи тільки шум? Прийняття рішення про наявність повідомлення – це і є його виявлення. Виявлення пов’язане з вимірюванням тих, чи інших параметрів прийнятого сигналу у очікуваних інтервалах значень. Інтервали, у яких зосереджені ці значення, характеризують точність, з якою вони визначаються (наприклад, точність визначення відстані у оглядовому локаторі та у локаторі наведення зброї).

Якщо ми спроможні відрізнити наявність повідомлення від його відсутності, ми маємо можливість передавати інформацію за допомогою двійкового коду. Наявність повідомлення буде відповідати символу 1, а відсутність – символу 0. Такий спосіб передавання інформації має назву передавання з пасивною паузою, бо у паузі передавач не працює.

Під час передавання двох різних повідомлень 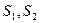мова йде про спосіб їх розрізнення. Розрізнення сигналів можна звести до відповіді на запитання: чи є на вході приймача суміш 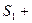шум, чи + шум? Відповідь на це питання залежить не тільки від властивостей окремих сигналів, а й від фізичних відмінностей між ними. Під час вибору сигналів слід прагнути до того, щоб відмінність між ними була стійкою до впливів завад і легко виявлялася наявними схемотехнічними засобами. Передавання двійковим кодом, у якому символу 1 відповідає сигнал 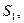а символу 0 – сигнал , називається передаванням з активною паузою.

Завдання відновлення повідомлення полягає у тому, щоб одержати вихідний сигнал 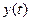, що найменшим чином відрізняється від переданого 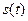. Суттєвим є те, що повідомлення заздалегідь невідоме, що дозволяє його розглядати як одну з реалізацій деякого випадкового процесу. Відповідно, заздалегідь відомими можуть бути закон розподілу або моменти розподілу ймовірностей цього процесу та його середній енергетичний спектр (це, наприклад, радіомовлення, телебачення тощо). Під час відновлення повідомлення слід спиратися на критерій якості відновлення. Цей критерій визначається вимогами до конкретного виду повідомлень.

Найчастіше використовується квадратичний критерій

тобто вводиться обмеження на середньоквадратичне відхилення сигналу від еталону на інтервалі існування 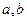. Цей критерій використовують, наприклад, для визначення якості передавання мовлення. Іноді користуються критерієм мінімуму максимального відхилення

тобто обмежується максимальна відміннсть прийнятого сигналу від еталону. Цей критерій використовують, наприклад, для визначення якості передавання зображення.

Однією з найважливіших характеристик будь-якої системи передавання інформації є її завадостійкість , тобто спроможність виконувати основну функцію під впливом завад. Дія завади проявляється у тому, що прийняте повідомлення відрізняється за формою від переданого. Тому завадостійкість можна оцінювати степінню відповідності прийнятого та переданого сигналів при заданому рівні завад. Кількісна міра відповідності залежить від характеру повідомлення – дискретного або аналогового.

Дискретне повідомлення є послідовністю символів з деякої скінченої множини, про яку відома ймовірність появи тих, чи інших символів. Вплив завади у цьому випадку проявляється у заміні одного символу іншим. Така подія називається помилкою. Поява помилки є випадковою, тому кількісною мірою завадостійкості можуть бути ймовірність помилки 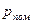, або ймовірність вірного приймання , бо помилка та вірне приймання утворюють повну групу подій. Користуються також вірністю передавання

.

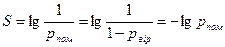У випадку аналогового повідомлення відмінність прийнятого повідомлення від переданого має неперервний характер. Якщо передане повідомлення подати у вигляді багатовимірного вектора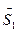, то в результаті дії завади одержимо вектор прийнятого повідомлення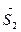, який відрізняється від першого довжиною та напрямом. У цьому випадку ймовірність вірного приймання можна подати як ймовірність потрапляння кінця вектора прийнятого повідомлення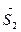у сферу радіусу 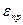, окреслену навколо кінця вектора переданого повідомлення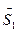

Читайте також:

1. I. ОБРАЗОВАНИЕ СОЕДИНЕННЫХ ШТАТОВ 14 страница
2. А. В. Дудник 1 страница
3. А. В. Дудник 10 страница
4. А. В. Дудник 11 страница
5. А. В. Дудник 12 страница
6. А. В. Дудник 2 страница
7. А. В. Дудник 3 страница
8. А. В. Дудник 4 страница
9. А. В. Дудник 5 страница
10. А. В. Дудник 6 страница
11. А. В. Дудник 7 страница
12. А. В. Дудник 8 страница

Переглядів: 1160