Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Приклад 2 4 страница

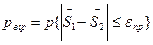Двовимірний випадок цього співвідношення поданий на Рис. 10.36. Координатами можуть бути інформаційні параметри сигналу (частота, напрям, затримка тощо), які, власне, і несуть повідомлення. Наведені міркування стосуються нормованих за амплітудою коливань, тобто виключається підсилення або ослаблення сигналу у каналі зв’язку.

Рішення щодо виявлення або розрізнення сигналів приймається за результатами спостереження реалізації суміші сигналу з шумом та завадами протягом тривалості реалізації 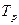. При цьому вважаються відомими закони розподілу ймовірностей значень напруги у каналі як за наявності тільки шуму, так і за наявності суміші сигналу з шумом (див Рис. 10.37). Результат спостереження 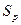є випадковою величиною або випадковим вектором, тому рішення буде мати ймовірнісний характер. Можливі чотири варіанти рішення щодо виявлення сигналу:

вважати, що сигналу немає за умови його відсутності;
вважати, що сигнал є за умови його наявності;
вважати, що сигналу немає, коли він присутній;
вважати, що сигнал є за умови його відсутності.

Перші два варіанти рішення є вірними, у третій та четвертий – хибними. Метод прийняття рішення повинен мінімізувати ризик схибити, тобто обрати варіант, який з більшою ймовірністю буде вірним. Для цього зручно користуватися величиною, що називається відношенням правдоподібності

та порівнювати її з обраним пороговим значенням 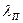. Якщо приймається рішення про наявність сигналу, якщо - про його відсутність.

Вибір значення 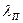залежить від конкретних умов, до яких можна віднести:

- наявність інформації щодо ймовірності появи сигналів;

- оцінку вартості прийняття вірних або хибних рішень.

У випадку приймання телеграфних повідомлень, коли ймовірність появи одиниці або нуля є однаковою, тоді Якщо ймовірність появи одиниці дорівнює 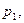а появи нуля, відповідно 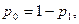поріг прийняття рішення буде 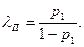Наведені правила прийняття рішення називаються критерієм ідеального спостерігача або критерієм Ригерта-Котельникова.

Якщо можна оцінити втрати від хибних рішень, застосовують критерій Байєса

де - умовні втрати, що відповідають хибним рішенням за третім та четвертим варіантами.

Під час виявлення радіолокаційних сигналів користуються критерієм Неймана-Пірсона, який полягає у наступному. Прийнятий сигнал порівнюється з пороговим значенням, яке визначається, виходячи з таких умов. Головною помилкою, яка називається пропуск цілі, вважається четвертий варіант, тобто твердження, що сигналу немає, коли він є. Ймовірність цієї помилки визначається, виходячи із заданої ймовірності третього варіанту 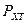, що називається хибною тривогою .Поріг порівняння визначається із співвідношення

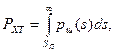
а далі, ймовірність пропуску цілі 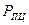визначають інтегруванням розподілу суміші сигналу з шумом.

Рис. 10.38 илюструє подані співвідношення. Поріг визначається експериментально для конкретного коефіцієнту шуму приймача. У реальних умовах для виявлення та розрізнення сигналів визначають не відношення правдоподібності, а логарифмічну функцію від нього, що дозволяє обчислювати матсподівання реалізації та порівнювати його з перерахованим значенням порогу.

Зрозуміло, що ймовірність вірного виявлення та розрізнення сигналів збільшуються із зростанням відношення сигнал/шум. Тому актуальним є завдання максимально збільшити його до початку приймання рішення щодо сигналів. Головна ідея такого оброблення суміші сигналу з шумом, що називається оптимальною фільтрацією, полягає у підсумовуванні енергії сигналу, розподіленої зазделегідь відомим способом за часом, частотою, напрямом тощо. Таким чином використовується відома структура сигналу «в цілому» з урахуванням функціональної залежності між його розподіленими частинами. На відміну від сигналу, шуми та завади мають випадковий характер, завдяки чому, під час підсумовування додаються їхні дисперсії. У підсумку, на виході оптимального фильтра елементи сигналу підсумовуються арифметично, а елементи шуму середньоквадратично. Суттєвою особливістю оптимального фільтра є та, що сигнал на його виході набуває найбільшого значення (відповідно, з найбільшим відношенням сигнал/шум) наприкінці дії вхідного сигналу, тобто форма вихідного сигналу може суттєво відрізнятися від форми вхідного. Приклад такого найпростішого оптимального фільтра подано на Рис. 10.39. Він обробляє сигнал у вигляді серії прямокутних імпульсів відомої тривалості, з відомими паузами між ними. Процедура фільтрації полягає у підсумовуванні імпульсів серії, 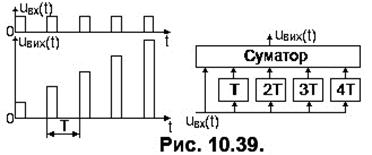затриманих у відповідності до тривалості їх затримки у вхідному сигналі. У підсумку, в момент надходження чергового імпульсу, на виході діє підсумковий імпульс, амплітуда якого дорівнює сумі амплітуд імпульсів, що вже надійшли на вихід. Найбільший вихідний імпульс буде наприкінці всієї серії.

Оптимальну фільтрацію широко застосовують для розрізнення двійкових сигналів, використовуючи технологію розширення спектра, яка полягає у наступному. У передавачі інформаційним символам 1 та 0, які мають тривалість 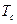, протягом тривалості символу передають кодові послідовності нулів та одиниць, які мають такі властивості:

- тривалість одного символу 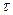кодової послідовності значно менше 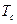, тобто ширина спектра послідовності відповідно розширюється;

- коди послідовностей, що відповідають 1 та 0, мають суттєві відмінності (наприклад, вони інвертовані одна відносно одної, тобто одиницям однієї послідовності відповідають нулі іншої).

У приймачі встановлюють оптимальні фільтри для «одиничної» та «нульової» послідовностей, структура яких подібна, показаній на Рис. 10.39. Відносна амплітуда імпульсу на виході фільтра (у разі узгодженості його структури із структурою коду символу) в кінці символу дорівнює

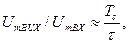
тобто відбувається суттєве збільшення амплітуди і зменшення тривалості вихідного імпульсу порівняно з вхідним. Для іншого коду накопичення на виході фільтра не відбувається. Рівні сигналів на виходах фільтрів наприкінці символу порівнюются між собою і, в залежності від їх співвідношення, приймається рішення про наявність одиниці чи нуля на вході приймача. Система зв’язку потребує синхронізації, тобто фіксації моментів запуску кодових послідовностей у фільтри та моментів порівняння вихідних напруг фільтрів. Для синхронізації використовується або окремий канал, або кожному символу надається стійка ознака його початку у вигляді допоміжної кодової послідовності (преамбули).

Для неперервного повідомлення оптимальним буде фільтр, що мінімізує відхилення форми прийнятого сигналу від переданого. Для створення такого фільтра неодхідна інформація про часові або частотні властивості і сигналів, і завад. За умови мінімізації середньоквадратичного відхилення, можна одержати АЧХ так званого Вінерівського фільтра

де - енергетичні спектри сигналу та завади. Такий фільтр фізично реалізувати не можна, але його сенс є абсолютно прозорим – фільтр повинен мати АЧХ з максимумами в частотних областях, де зосереджено найбільшу потужність сигналу, і мінімуми - в областях дії завад.

10.12. Підсумки та самоконтроль

Розділ присвячений вивченню можливостей моделювання сигналів за допомогою періодичних та неперіодичних функцій. Розглянуто розкладання коливання складної форми на простіші за допомогою ряду та інтегралу Фур’є. Сформульовано основні властивості спектрів періодичних та неперіодичних коливань, а також зв’язок між часовими та частотними характеристиками коливань. Наведено методику розрахунку спектрів імпульсних коливань без безпосереднього використання перетворення Фур’є.

У розділі коротко розглянуті основні характеристики випадкових процесів, які моделюють шуми і завади, що виникають під час приймання повідомлень. Наведено параметри випадкових процесів у часовій та частотній областях, які дозволяють оцінювати їхній вплив на якість та вірогідність прийнятого повідомлення. Виконано огляд методів завадостійкого приймання сигналів.

Поглибити знання за тематикою цього розділу можна, скориставшись літературою [2, p. 6, р. 7.1,], [3, гл. 7, 9, 12], [5, гл. 18, 19], [7, р. 4.5, 4.6].

Проконтролювати засвоєння матеріалу цього розділу можна, відповівши на такі питання:

1. Які коливання використовуються для моделювання сигналів?

2. Наведіть параметри синусоїдного коливання.

3. Який зв’язок існує між функцією ввімкнення та дельта-функцією?

4. Які основні властивості дельта-функції?

5. Яку функцію можна розкласти в ряд Фур’є?

6. Запишіть ряд Фур’є у тригонометричній та комплексній формі.

7. Який зміст має від’ємна частота?

8. Чому спектр періодичного коливання є лінійчатим?

9. Запишіть пряме та обернене перетворення Фур’є.

10. Який фізичний зміст спектральної густини?

11. Як пов’язані між собою спектри неперіодичного та періодичного коливань?

12. Чому дорівнює дієве значення та потужність періодичного струму?

13. Чому дорівнює енергія неперіодичного струму?

14. Які основні властивості спектрів коливань?

15. Який зв’язок між часовими та спектральними характеристиками коливань?

16. Які параметри описують випадкові процеси?

17. Що таке «білий шум»?

18. Яка еквівалентна схема опору, що шумить?

19. Що таке відношення правдоподібності?

20. За якими критеріями приймається рішення про виявлення сигналу?

21. Яка інформація про сигнал та заваду необхідна для побудови оптимального фільтра?

11. МОДУЛЬОВАНІ КОЛИВАННЯ

11.1. Частотні характеристики повідомлень

Радіоелектронні пристрої оброблюють повідомлення, які є струмами і напругами на виходах вимірювальних перетворювачів (механічних, акустичних, оптичних, хімічних тощо). Ці струми і напруги змінюються пропорційно силі та швидкості дій на входах перетворювачів (звуковий тиск, колір та інтенсивність світла тощо). Частотний діапазон змін дії у повідомленнях різний, однак всі вони мають спільну ознаку, а саме – широкосмуговість, тобто велику різницю між значеннями верхньої та нижньої граничних частот. Ця характеристика описується коефіцієнтом широкосмуговості

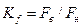. (11.1)

У Таблиці 1 наведено кілька прикладів найпоширеніших повідомлень, що використовуються повсякденно.

Таблиця 1

Повідомлення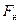
звук	20 Гц	20 кГц	10³
ультразвук	100 кГц	10 МГц	10²
відео	50 Гц	6,5 МГц	1,3.10⁵
біосигнал	0,01 Гц	500 Гц	5.10⁴

Сигнали, що переносять повідомлення і мають , називаються інформаційними (аудіо-, відео-, біо- в залежності від джерела їх походження) і мають спільну назву широкосмугові сигнали.

11.2. Загальні вимоги до систем передавання та приймання інформації

Під час розроблення систем передавання та приймання повідомлень необхідно розв’язати ряд складних завдань. Серед них:

забезпечити можливість розділення одночасно існуючих повідомлень, надаючи їм стійкі ознаки розрізнення;
забезпечити ефективне передавання та приймання усіх частотних складових повідомлення, враховуючи його широкосмуговість;
формувати сигнали, що переносять повідомлення таким чином, щоб вони не заважали передаванню та прийманню інших повідомлень, що існують одночасно.

Передавання та приймання повідомлень відбувається у каналах зв’язку, тобто у фізичному середовищі, у якому відбувається поширення сигналів. У радіоелектроніці використовуються провідні, ефірні та оптичні канали, у яких поширюються ЕМХ. Випромінювання ЕМХ відбувається ефективно, коли розміри випромінювачів дорівнюють часткам довжини ЕМХ . Тобто реалізація ефективних випромінювальних (антенних) систем можлива на достатньо високих частотах, відповідно, на малих довжинах хвиль. Задача ускладнюється необхідністю випромінювання з однаковою ефективністю широкосмугових коливань з достатньо низькими частотами, тобто з великими довжинами хвиль (див. Таблицю 1). Тому постає завдання сформувати сигнал таким чином, щоб він відповідав усім наведеним вимогам. Такий сигнал називається радіосигналом і найчастіше є синусоїдним коливанням із змінними параметрами.

11.3. Загальні властивості радіосигналів

Технічно найпростіше одержати високочастотне синусоїдне коливання. У найбільш загальному вигляді це коливання подається виразом

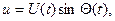(11.2)

де 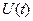та - закони зміни амплітуди та фази коливання.

Зробимо заміни

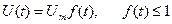та 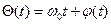, (11.3)

де 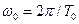- середня частота коливання (2), яка може використовуватись як стійка ознака цього коливання, 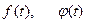- функції, що мало змінюються за тривалість періоду , тобто їхня швидкість зміни значно менша за швидкість зміни коливання з частотою 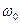. Умови відносної повільності мають вигляд

(11.4)

Форма спектра коливання (2) залежить від законів зміни 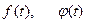, але, враховуючи, що ширина спектра коливання обернено пропорційна його тривалості або швидкості його зміни, можна стверджувати, що у разі виконання умов (4), частота 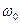буде значно більшою за ширину спектра цього коливання. Коливання, що відповідають умовам (4), на відміну від інформаційних (широкосмугових) називаються вузькосмуговими або радіосигналами. У радіосигналі

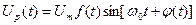(11.5)

можуть відносно повільно змінюватися два параметри – амплітуда та фаза. Причому, можливі як роздільні так і одночасні зміни цих параметрів за однаковими або різними законами. Головна властивість радіосигналу полягає в тому, що незалежно від того, які параметри змінюються, енергію сигналу зосереджено поблизу частоти що називається носійною частотою або частотою носійного коливання. Відповідно, обираючи різні значення носійних частот за умови

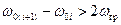(11.6)

можна одночасно передавати необхідну кількість повідомлень без їх взаємного впливу. Такий спосіб одночасного передавання та приймання повідомлень, поданий на Рис. 11.1, називається частотним ущільненням (розділенням) каналів передавання інформації.

11.4. Види модульованих коливань

Модуляцією називається процес зміни параметрів коливання відповідно до зміни миттєвих значень повідомлення. Зміна амплітуди носійного коливання називається амплітудною модуляцією (АМ). Зміна фази носійного коливання у загальному випадку називається кутовою модуляцією (КМ), яку за характером зміни фази можна розділити на частотну (ЧМ) та фазову (ФМ). Часто використовують одночасну зміну і амплітуди, і фази носійного коливання.

11.4. 1. Амплітудна модуляція

Коливання з модульованою амплітудою має вигляд

(11.7)

де - амплітуда, частота та фаза носійного коливання;

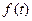- закон зміни миттєвих значень повідомлення, що передається;

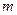- глибина модуляції - - відношення максимального приросту амплітуди коливання за рахунок модуляції до значення амплітуди за відсутності модуляції.

У найпростішому випадку модуляції косинусоїдним коливанням

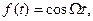(11.8)

де 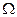- частота модуляції, АМ коливання має вигляд, поданий на Рис. 11.2 згори

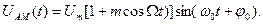(11.9)

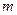З визначення маємо

(11.10)

Виконаємо перетворення виразу (9)

(11.11)

Спектр цього коливання (Рис. 11.2, знизу)

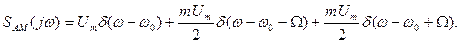(11.12)

Таким чином, у спектральній області ефект амплітудної модуляції може бути описаний як додавання до носійного коливання пари синусоїдних коливань, які називаються бічними та мають частоти, що відрізняються від частоти носійного на 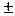частоту модуляції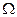. Слід зазначити, що спектр АМ коливання не має гармонічних властивостей, бо між частотами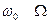

немає ніякого зв’язку. Векторна діаграма АМ коливання для різних моментів часу має вигляд, поданий на Рис. 11.3. За рахунок взаємного положення векторів бічних коливань та носійного сума трьох векторів будь-якої миті утворює вектор, напрям якого співпадає з напрямом вектора носійного коливання, тобто є наявним АМ коливання.

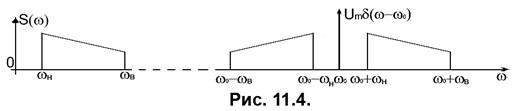У загальному випадку модуляції складною функцією що має спектр частот, обмежений частотами 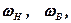АМ коливання містить дві бічні смуги частот, розташовані симетрично відносно частоти носійного коливання (див. Рис. 11.4). Вісь частот у середній частині рисунку намальовано пунктиром, що повинно підкреслити основну властивість модульованого коливання – його вузькосмуговість, тобто виконання умови

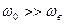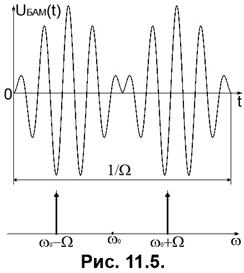
Таким чином, результатом амплітудної модуляції є коливання, обвідна якого повторює закон зміни миттєвих значень повідомлення, а у спектрі АМ коливання є верхня та нижня бічні смуги, причому верхня бічна смуга повторює за формою спектр повідомлення, а нижня є її дзеркальною копією. З Рис. 11.4 видно, що спектр АМ коливання є надлишковим – з точки зору передавання інформації зайвим є носійне коливання й одна з бічних смуг, на передавання яких витрачається зайва потужність передавача та смуга частот. Втрати потужності можна зменшити, використовуючи балансну амплітудну модуляцію (БАМ) – тобто АМ з відсутнім носійним коливанням, подану на Рис. 11.5. Часова функція БАМ має вигляд

(11.13)

Спектр БАМ має вигляд

(11.14)

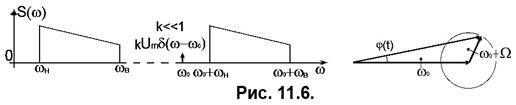Радіосигналом з найбільшою ефективністю використання смуги частот є сигнал з однією бічною смугою (ОБС) (див. Рис. 11.6). Векторну діаграму ОБС коливання під час модуляції однією синусоїдою подано на Рис. 11.6, праворуч. З рисунку видно, що коливання з ОБС фактично є коливанням з амплітудно-фазовою модуляцією, тобто у нього змінюється миттєве значення як модулю, так і фази вектору. Для спрощення приймання такого сигналу у його складі зберігають залишок носійного коливання, на яке налаштовується приймальний пристрій.

11.4.2. Кутова модуляція

Коливання з кутовою модуляцією має вигляд

(11.15)

Миттєва частота коливання є швидкістю зміни миттєвої фази

(11.16)

Тобто зміна фази коливання за законом 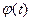призводить до зміни миттєвої частоти за законом похідної і навпаки. За умови незмінної частоти, фаза змінюється лінійно 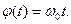На Рис. 11.7 подано лінійний закон модулювальної функції 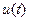і відповідний йому закон зміни фази 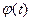. Диференціювання миттєвої фази призводить до стрибкоподібної зміни миттєвої частоти модульованого коливання між значеннями та 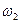. На нижньому рисунку подане це коливання, що має сталу амплітуду і два послідовно змінних значення частоти.

У КМ коливанні миттєва частота змінюється навколо середнього значення за законом

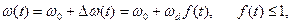
де - частотне відхилення або девіація частоти – максимальне відхилення частоти під час модуляції при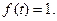

Миттєва фаза при цьому змінюється за законом

. (11.17)

У найпростішому випадку 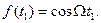Закон зміни фази

(11.18)

Підставивши вираз (18) у (15), одержимо

(11.19)

Величина 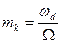називається індексом кутової модуляції. Він не залежить від носійної частоти і дорівнює максимальному відносному відхиленню фази вектора носійного коливання за період модуляції

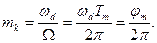(11.20)

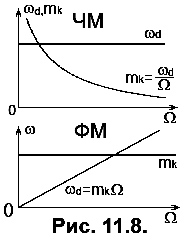ЧМ та ФМ коливання мають наступні відмінності (див. Рис. 11.8). Під час ЧМ значення девіації частоти є пропор- ційним амплітуді інформаційної функції (тобто, чим гучніше звук, тим більше частотне відхилення у разі ЧМ мовлення) і не залежить від частоти модуляції 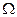. Під час ФМ індекс модуляції є пропорційним амплітуді інформаційної функції і не залежить від частоти модуляції . Залежності на

Рис.11.8 подані для сталої амплітуди модулювальної функції. У разі сталих значень амплітуди і частоти інформаційної (модулювальної) функції розрізнити ЧМ та ФМ неможливо.

Для визначення спектра КМ коливання зробимо перетворення виразу (19)

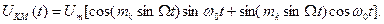(11.21)

Розглянемо спочатку випадок 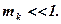За цієї умови

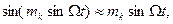
Тоді 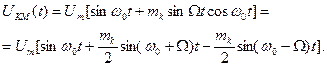(11.22)

Спектр цього коливання має вигляд

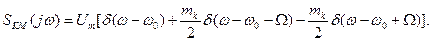(11.23)

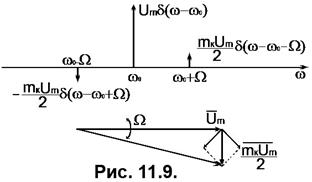
Порівнюючи його із спектром АМ коливання (12), бачимо, що вони відрізняються протилежним знаком коливання нижньої бічної частоти, тобто комплексний спектр і векторна діаграма коливання з КМ мають вигляд, поданий на Рис. 11. 9. З розгляду векторної діаграми видно, що вектор КМ коливання обертається із змінною швидкістю, гойдаючись з частотою модуляції відносно середнього значення . Зміною довжини вектора, тобто амплітуди КМ коливання за умови можна знехтувати.

У разі збільшення картина спектра суттєво ускладнюється, тому що

(13.23)

де - функція Бесселя першого роду к-го порядку від аргументу, показана на Рис. 11.10. Спектр КМ-коливання у цьому випадку є нескінченною сумою бічних складових, частоти яких йдуть з інтервалом, що дорівнює частоті модуляції 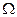. При різних значеннях функції змінюють знак, що свідчить про зміну фази складових спектра на 180⁰. Із зростанням амплітуди складових зменшуються і, за умови , основна частина енергії коливання зосереджується у смузі частот навколо частоти . 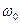Внаслідок цього, сигнал з кутовою модуляцією за умови 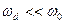теж є вузькосмуговим, тобто відповідає вимогам до радіосигналів. На Рис. 11.11 подано кілька спектральних діаграм КМ коливань, на яких співвідношення між складовими відповідають графікам, поданим на Рис. 11.10. Зміна параметру відбувалася за рахунок зменшення модулювальної частоти 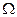при сталому значенні .

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Приклад 2 3 страница	\|	Приклад 2 5 страница

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.011 сек.