
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Приклад 2 5 страница
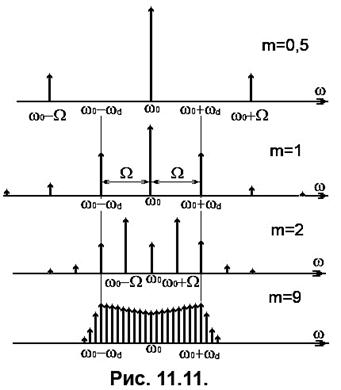 Порівнюючи характеристики спектрів і миттєвих значень коливань для різних видів модуляції при синусоїдній інформаційній функції, можна зробити наступні висновки:
Порівнюючи характеристики спектрів і миттєвих значень коливань для різних видів модуляції при синусоїдній інформаційній функції, можна зробити наступні висновки:
1. Спектри модульованих коливань завжди ширше за спектр модулювальної функції (за винятком коливання ОБС).
2. Миттєві значення обвідної АМ коливання повторюють миттєві значення інформаційної функції. Спектр АМ сигналу є симетричним відносно частоти носійного коливання, ширина його удвоє перевищує ширину спектра повідомлення, причому друга бічна смуга та носійне коливання додаткової інформації не несуть.
3. Спектр КМ коливання має більш складну структуру, ніж спектр повідомлення, його склад і зайнята смуга залежить від виду та індексу модуляції.
4. При ЧМ поточна ширина спектра сигналу в основному залежить від значення девіації частоти 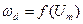 (чим гучніше звук, тим ширше спектр), а кількість спектральних складових - від індексу модуляції (
(чим гучніше звук, тим ширше спектр), а кількість спектральних складових - від індексу модуляції (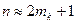 ), тобто від частотних характеристик повідомлення. Наприклад, для ЧМ радіомовлення стандартне значення девіації частоти
), тобто від частотних характеристик повідомлення. Наприклад, для ЧМ радіомовлення стандартне значення девіації частоти 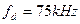 , для діапазону звукових частот
, для діапазону звукових частот 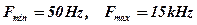 маємо
маємо 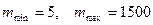 , відповідно
, відповідно  .
.
5. При ФМ кількість складових залишається незмінною, але змінюється відстань між ними, що залежить від частоти модуляції 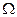 . Тобто поточна ширина спектра ФМ сильно змінюється в залежності від частотного складу повідомлення ( чим вище звук, тим ширше спектр).
. Тобто поточна ширина спектра ФМ сильно змінюється в залежності від частотного складу повідомлення ( чим вище звук, тим ширше спектр).
6. Враховуючи, що діапазон використовуваних частот розбито на однакові за шириною смуги, що надаються різним джерелам повідомлень, зручніше користуватися частотною модуляцією, що порівняно з фазовою, має більшу ефективність використання наданої смуги частот.
7. Розрізнити ЧМ та ФМ за умови сталих амплітуди і частоти інформаційного коливання неможливо. Різниця виникає тільки під час зміни параметрів модулювальної функції.
11.5. Маніпульовані коливання
У розділі 11.1 були розглянуті властивості аналогових повідомлень, тобто таких, які приймають будь-яке значення у заздалегідь обумовлених межах. Усі вони мали спільну властивість – широкосмуговість, тому, для забезпечення їхнього ефективного передавання та приймання, було запропоновано використати модуляцію – перенесення повідомлення на високу носійну частоту.
Широкий клас повідомлень має імпульсну природу, тобто являє послідовність найчастіше прямокутних імпульсів, які мають тільки два значення – одиницю та нуль. Спектр такого коливання теоретично необмежений, крім того містить сталу складову. Тому такі повідомлення не можуть бути безпосередньо передані каналом з частотним ущільненням. Для одночасного передавання дискретних повідомлень їхній спектр необхідно, по-перше, обмежити за частотою, по-друге, перенести у діапазон більш високих частот, тобто застосувати модуляцію. Модуляція ВЧ коливання імпульсами прямокутної форми називається маніпуляцією. Змінні параметри ВЧ коливання приймають при цьому обмежену кількість значень, найчастіше – два, що відповідають наявності та відсутності імпульсу. Розглянемо часові та частотні характеристики маніпульованих коливань у найпростішому випадку, коли модулювальна функція є періодичною послідовністю прямокутних імпульсів з однаковою тривалістю імпульсів та пауз між ними. Така послідовність має жаргонну назву „меандр” і описується виразом
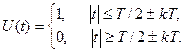 (11.24)
(11.24)
Спектр періодичної послідовності прямокутних імпульсів було визначено у розділі 10.4 і, за умови 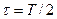 , послідовність (24) можна подати у вигляді
, послідовність (24) можна подати у вигляді
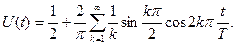 (10.25)
(10.25)
Амплітудно маніпульоване (АМн) коливання є результатом множення інформаційного коливання на коливання носійної частоти і має вигляд, поданий на Рис. 11.12,а
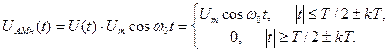 (10.26)
(10.26)
АМн коливання часто називають телеграфним сигналом з пасивною паузою, бо під час передавання нулів повідомлення коливання не випромінюється. Підставимо вираз (25) до виразу (26) і одержимо частотний склад АМн коливання
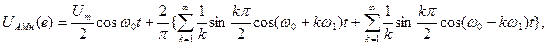 (10.27)
(10.27)
 |
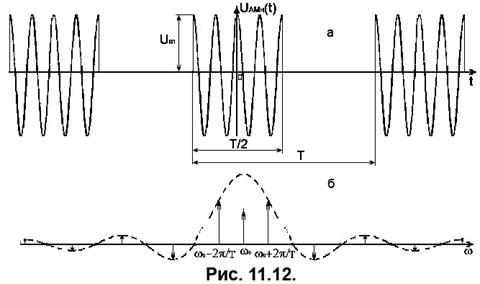 тобто у частотній області спектр АМн коливання відтворює спектр періодичної послідовності прямокутних імпульсів, зсунутий на частоту носійного коливання (див. Рис. 11.12,б) . Слід зазначити, що, враховуючи нескінченність спектра імпульсу під час перенесення його на носійну частоту, відбувається деяке спотворення форми спектра у вигляді його асиметрії відносно середньої частоти. Ефект викликаний «перекриттям» спектрів із області додатних та від’ємних частот, або дзеркального «перегинання» «хвоста» спектра відносно нуля частот. Цим спотворенням можна знехтувати за умови
тобто у частотній області спектр АМн коливання відтворює спектр періодичної послідовності прямокутних імпульсів, зсунутий на частоту носійного коливання (див. Рис. 11.12,б) . Слід зазначити, що, враховуючи нескінченність спектра імпульсу під час перенесення його на носійну частоту, відбувається деяке спотворення форми спектра у вигляді його асиметрії відносно середньої частоти. Ефект викликаний «перекриттям» спектрів із області додатних та від’ємних частот, або дзеркального «перегинання» «хвоста» спектра відносно нуля частот. Цим спотворенням можна знехтувати за умови 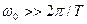 .
.
Фазово маніпульоване коливання (ФМн) можна розглядати як суму двох АМн коливань однакової частоти з різними початковими фазами, тобто
 (10.28)
(10.28)
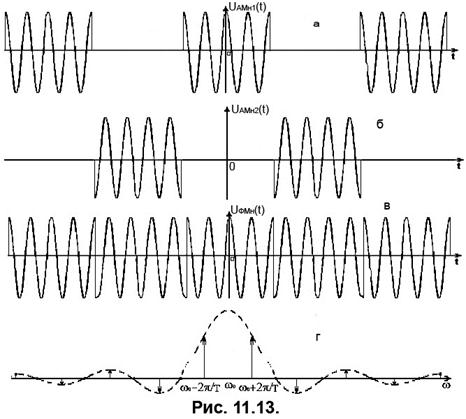
Найпростіший і досить часто вживаний випадок, коли 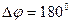 . Часову діаграму для цього випадку подано на Рис. 11.13, а,б,в. Визначимо частотний склад ФМн коливання для цього випадку. Для цього підставимо у вираз (28) розклад модулювальної функції (25) і заданий зсув фаз. Після перетворень одержимо
. Часову діаграму для цього випадку подано на Рис. 11.13, а,б,в. Визначимо частотний склад ФМн коливання для цього випадку. Для цього підставимо у вираз (28) розклад модулювальної функції (25) і заданий зсув фаз. Після перетворень одержимо
 (10.29)
(10.29)
тобто спектр ФМн коливання, за умови 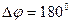 , відрізняються від АМн відсутністю носійного коливання, скомпенсованого за рахунок додавання двох АМн коливань. Спектр для цього випадку поданий на Рис. 11.13,г.
, відрізняються від АМн відсутністю носійного коливання, скомпенсованого за рахунок додавання двох АМн коливань. Спектр для цього випадку поданий на Рис. 11.13,г.
У випадку інших значень фазового зсуву між елементами повідомлення, форма обвідної спектра залишається незмінною, але з’являється носійне коливання, амплітуда якого тим більше, порівняно з бічними складовими, чим менше фазовий зсув. Якщо 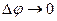 , спектр вироджується у одну
, спектр вироджується у одну 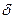 – функцію на частоті
– функцію на частоті 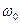 .
.
Частотно маніпульоване (ЧМн) коливання теж можна розглядати як суму двох зсунутих у часі АМн коливань, але з різними носійними частотами (див. Рис. 11.14,а)
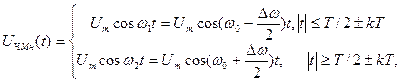 (11.30)
(11.30)
або
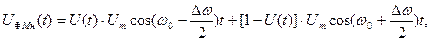
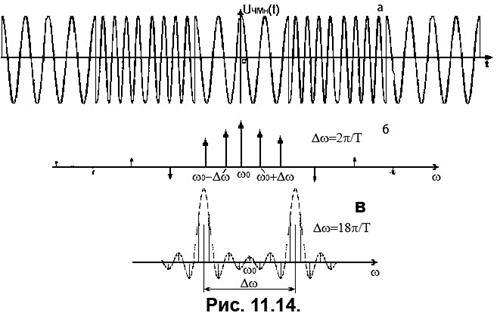 де
де  - частотний зсув між елементами повідомлення. Частотний склад цього коливання можна, як і раніше, розглядати як суперпозицію складових двох АМн коливань. Форма обвідної спектра ЧМн коливання залежить від співвідношення між значеннями
- частотний зсув між елементами повідомлення. Частотний склад цього коливання можна, як і раніше, розглядати як суперпозицію складових двох АМн коливань. Форма обвідної спектра ЧМн коливання залежить від співвідношення між значеннями  і
і 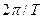 . Розрізняють «швидку», або «вузькосмугову» ЧМн, коли
. Розрізняють «швидку», або «вузькосмугову» ЧМн, коли 
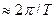 , та «повільну», або «широкосмугову» ЧМн, коли
, та «повільну», або «широкосмугову» ЧМн, коли 
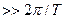 . У першому випадку форма спектра коливання майже не відрізняється від спектрів АМн та ФМн, у другому – наближається за формою до спектру суми двох незалежних АМн коливань. Спектри для цих двох випадків подано на Рис. 11.14,б,в.
. У першому випадку форма спектра коливання майже не відрізняється від спектрів АМн та ФМн, у другому – наближається за формою до спектру суми двох незалежних АМн коливань. Спектри для цих двох випадків подано на Рис. 11.14,б,в.
Теоретично спектр імпульсного коливання нескінченний за частотою. У реальних каналах зв’язку для обмеження ширини спектра маніпульованих коливань застосовують згладжування обвідної сигналу та вилучають стрибки коливання під час переходу від символу до символу сигналу. ЧМн та ФМн коливання називають телеграфними сигналами з активною паузою, бо коливання випромінюється під час передавання обох символів – і одиниці, і нуля.
11.6. Імпульсна модуляція коливань
 Основним завданням розглянутих видів модуляції є перенесення повідомлення на високу фіксовану носійну частоту з метою одночасного передавання багатьох повідомлень на різних носійних частотах. Але забезпечити одночасне передавання багатьох повідомлень можна в інший спосіб, послідовно передаючи миттєві значення повідомлень у різні, не співпадаючі, моменти часу. На рис. 11.15. показана можливість передавання двох незалежних повідомлень одним каналом зв’язку з часовимущільненням (розділенням) каналів. Як видно з рисунку, для забезпечення такого виду багатоканального зв’язку, необхідно виконати перетворення аналогового повідомлення на періодичну послідовність коротких імпульсів, амплітуда яких (або інший параметр послідовності) змінюється за законом повідомлення. Власне імпульсні послідовності виконують роль носійних коливань. Процес такого перетворення називається імпульсною модуляцією. Використовуючи кілька імпульсних послідовностей однієї частоти, але зсунутих за часом, можна сформувати багатоканальний сигнал. На Рис. 11.15. показано дві послідовності амплітудно-модульованих (АІМ) імпульсів. Широко застосовують частотно-імпульсну (ЧІМ), широтно-імпульсну (ШІМ) та інші види модуляції параметрів імпульсних послідовностей.
Основним завданням розглянутих видів модуляції є перенесення повідомлення на високу фіксовану носійну частоту з метою одночасного передавання багатьох повідомлень на різних носійних частотах. Але забезпечити одночасне передавання багатьох повідомлень можна в інший спосіб, послідовно передаючи миттєві значення повідомлень у різні, не співпадаючі, моменти часу. На рис. 11.15. показана можливість передавання двох незалежних повідомлень одним каналом зв’язку з часовимущільненням (розділенням) каналів. Як видно з рисунку, для забезпечення такого виду багатоканального зв’язку, необхідно виконати перетворення аналогового повідомлення на періодичну послідовність коротких імпульсів, амплітуда яких (або інший параметр послідовності) змінюється за законом повідомлення. Власне імпульсні послідовності виконують роль носійних коливань. Процес такого перетворення називається імпульсною модуляцією. Використовуючи кілька імпульсних послідовностей однієї частоти, але зсунутих за часом, можна сформувати багатоканальний сигнал. На Рис. 11.15. показано дві послідовності амплітудно-модульованих (АІМ) імпульсів. Широко застосовують частотно-імпульсну (ЧІМ), широтно-імпульсну (ШІМ) та інші види модуляції параметрів імпульсних послідовностей.
Періодичну послідовність 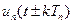 можна описати виразом
можна описати виразом
 (11.31)
(11.31)
де амплітуди і фази гармонік залежать від форми імпульсів у послідовності. Найчастіше використовують послідовність прямокутних імпульсів. Спектр такої послідовності розглянуто у попередньому розділі.
Розглянемо властивості АІМ для випадку гармонічної модулювальної функції 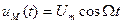 . Саме цей випадок показаний у верхній частині Рис. 11.15. Під час формування багатоканального сигналу зручно користуватися імпульсами тільки однієї полярності. Для цього у модулювальну функцію додають сталу складову, виходячи з умови
. Саме цей випадок показаний у верхній частині Рис. 11.15. Під час формування багатоканального сигналу зручно користуватися імпульсами тільки однієї полярності. Для цього у модулювальну функцію додають сталу складову, виходячи з умови
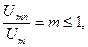
де 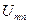 - амплітуда носійної послідовності імпульсів.
- амплітуда носійної послідовності імпульсів.
За цієї умови амплітудно-модульована послідовність описується виразом
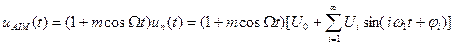 (11.32)
(11.32)
Частотний склад АІМ коливання одержимо, розкриваючи прямокутні дужки у виразі (32). У підсумку одержимо ряд, що містить складові такого виду

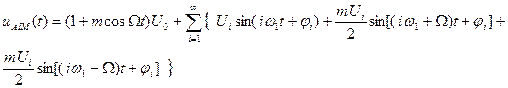 (11.33)
(11.33)
 Таким чином, спектр АІМ (див. Рис. 11.16) має обвідну, що повторює обвідну немодульованої імпульсної послідовності і складається з нескінченної сукупності спектрів амплітудно-модульованих гармонік частоти слідування послідовності, тобто навколо кожної гармоніки утворилася пара бічних коливань з частотами
Таким чином, спектр АІМ (див. Рис. 11.16) має обвідну, що повторює обвідну немодульованої імпульсної послідовності і складається з нескінченної сукупності спектрів амплітудно-модульованих гармонік частоти слідування послідовності, тобто навколо кожної гармоніки утворилася пара бічних коливань з частотами 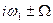 . Можна помітити деяку асиметрію бічних складових. Симетрія бічних залежить від характеру модуляції імпульсів. Можливі два варіанти модуляції – коли верхівка імпульсу повторює модулювальну функцію, або імпульс має незмінну амплітуду, що дорівнює миттєвому значенню модулювальної функції. У випадку, коли тривалість імпульсів послідовності значно менша за період модулювальної функції, можна знехтувати означеною асиметрією. Це реальний випадок, бо виконання вимоги
. Можна помітити деяку асиметрію бічних складових. Симетрія бічних залежить від характеру модуляції імпульсів. Можливі два варіанти модуляції – коли верхівка імпульсу повторює модулювальну функцію, або імпульс має незмінну амплітуду, що дорівнює миттєвому значенню модулювальної функції. У випадку, коли тривалість імпульсів послідовності значно менша за період модулювальної функції, можна знехтувати означеною асиметрією. Це реальний випадок, бо виконання вимоги 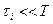 надає можливість багатоканального передавання інформації. Інформація міститься або у складовій з частотою
надає можливість багатоканального передавання інформації. Інформація міститься або у складовій з частотою 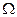 , або у бічних складових будь-якої гармоніки і може бути відтворена за допомогою фільтрації фільтром нижніх частот, у разі виділення складової з частотою
, або у бічних складових будь-якої гармоніки і може бути відтворена за допомогою фільтрації фільтром нижніх частот, у разі виділення складової з частотою 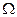 , або смуговим фільтром, у разі виділення складової з частотою
, або смуговим фільтром, у разі виділення складової з частотою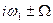 . У останньому випадку відфільтроване коливання буде мати вигляд АМ синусоїдного коливання з носійною частотою
. У останньому випадку відфільтроване коливання буде мати вигляд АМ синусоїдного коливання з носійною частотою 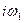 та частотою обвідної
та частотою обвідної 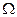 . Розділити коливання фільтром можливо у разі виконання умови
. Розділити коливання фільтром можливо у разі виконання умови  або
або 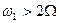 . У протилежному випадку спектри бічних складових перетинаються і не можуть бути розділені будь-яким способом.
. У протилежному випадку спектри бічних складових перетинаються і не можуть бути розділені будь-яким способом.
З Рис. 11.16 видно, що ширина спектра АІМ коливання мало залежить від параметрів повідомлення, а цілком визначається тривалістю імпульсів послідовності. Якщо застосувати періодичну послідовність з великими значеннями шпаруватості
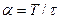 ,
,
з’являється можливість передавати одним каналом зв’язку багато повідомлень, що зсунуті одне відносно одного у часі. Стійкою ознакою розрізнення цих повідомлень стає часова затримка їх відліків відносно спільного для усіх каналів імпульсу синхронізації. Ефективність системи збільшується із збільшенням  . У сучасних багатоканальних системах
. У сучасних багатоканальних системах 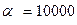 .
.
11.7. Дискретизація коливань
Сучасна апаратура передавання та приймання інформації (системи зв’язку, навігації, телебачення тощо) все частіше базується на принципах дискретного (цифрового) оброблення повідомлень з використанням комп’ютерної техніки. Незалежно від призначення така апаратура має спільні властивості, а саме:
- обмежену точність подання інформації (розрядність даних);
- обмежений об’єм запам’ятовуючих пристроїв, що накопичують миттєві значення повідомлень для їх оброблення.
 Аналоговий сигнал, тобто коливання, що переносить повідомлення, є неперервним, іншими словами, має нескінченну множину миттєвих значень, які можуть відрізнятись на нескінченно малу величину. Тобто для їх оброблення потрібна нескінченно велика точність подання. Для уникнення протиріччя між властивостями аналогових сигналів і можливостями дискретної апаратури їх оброблення застосовується дискретизація коливань - процес періодичного визначення миттєвих значень (відліків) цих коливань з обмеженою точністю і запам’ятовування послідовностей відліків.
Аналоговий сигнал, тобто коливання, що переносить повідомлення, є неперервним, іншими словами, має нескінченну множину миттєвих значень, які можуть відрізнятись на нескінченно малу величину. Тобто для їх оброблення потрібна нескінченно велика точність подання. Для уникнення протиріччя між властивостями аналогових сигналів і можливостями дискретної апаратури їх оброблення застосовується дискретизація коливань - процес періодичного визначення миттєвих значень (відліків) цих коливань з обмеженою точністю і запам’ятовування послідовностей відліків.
Під час дискретизації коливань, природно, втрачається деяка частка інформації, тобто форма повідомлення дещо змінюється. Вимоги до апаратури дискретизації зводяться до обмеження кількості цих втрат, щоб не призвести до руйнування інформації.
Розрізнюють дискретизацію коливання за рівнем (квантування), коли миттєві значення коливання замінюються найближчими дозволеними значеннями, та дискретизацію за часом, коли замість неперервного коливання одержують його вибіркові значення, взяті через заданий часовий інтервал. Процес одержання дискретизованих відліків повідомлення у вигляді синусного коливання подано на Рис. 11. 17. Різниця між миттєвими значеннями аналогового коливання та дискретизованими значеннями обмеженої точності називається шумом квантування і має вигляд періодичної послідовності імпульсів випадкової амплітуди, яка не перевищує 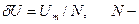 кількість можливих значень дискретизованого коливання.
кількість можливих значень дискретизованого коливання. 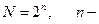 розрядність двійкових чисел, що подають миттєві значення.
розрядність двійкових чисел, що подають миттєві значення.
Будь-яке повідомлення є обмеженим у часі коливанням, іншими словами, це імпульсне коливання з нескінченним спектром. Але, обмеження ширини спектра смугою частот, що містить основну частину енергії коливання, призводить до спотворень, які можна задати, обираючи необхідну смугу частот для виконання конкретного інформаційного завдання (див. розд. 10.10). Отже, можна говорити про можливість передавання імпульсного коливання у обмеженій смузі частот із заданою якістю. Таким чином, для опису каналу зв’язку, необхідного для передавання повідомлення можна задати тривалість повідомлення, смугу необхідних частот та припустимі спотворення сигналу. За цих умов нема необхідності передавати всі підряд миттєві значення коливання, а можна обмежитись передаванням тільки вибіркових значень, частота вибору яких залежить від швидкості зміни повідомлення. Така можливість була доведена 1933 року В.І. Котельниковим у теоремі, яка стверджує наступне:
„ Функцію, що містить у своєму спектрі частоти від 0 до Fв можна з будь-якою точністю передати за допомогою відліків її миттєвих значень, що надходять один за одним з часовим інтервалом ТД < 2/FВ ”.
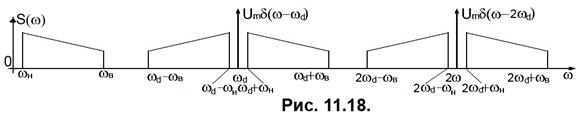 Фізичний зміст теореми Котельникова (теореми відліків) полягає в тому, функція з обмеженою верхньою граничною частотою має обмежену швидкість зміни і, відповідно, мало змінюється між моментами дискретизації. Відліки миттєвих значень коливання називаються його вибірками. Часовий інтервал між вибірками називається інтервалом дискретизації або інтервалом квантування за часом. Сукупність вибірок, що періодично надходить з періодом ТД утворює дискретизоване за часом коливання. Фактично, теорема Котельникова описує процес амплітудної модуляції періодичної послідовності
Фізичний зміст теореми Котельникова (теореми відліків) полягає в тому, функція з обмеженою верхньою граничною частотою має обмежену швидкість зміни і, відповідно, мало змінюється між моментами дискретизації. Відліки миттєвих значень коливання називаються його вибірками. Часовий інтервал між вибірками називається інтервалом дискретизації або інтервалом квантування за часом. Сукупність вибірок, що періодично надходить з періодом ТД утворює дискретизоване за часом коливання. Фактично, теорема Котельникова описує процес амплітудної модуляції періодичної послідовності 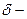 імпульсів, бо взяття вибірки ґрунтується на фільтрувальній властивості
імпульсів, бо взяття вибірки ґрунтується на фільтрувальній властивості 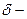 функції (див. вираз (10.20)). Теорема визначає умови, за яких з прийнятої споживачем модульованої імпульсної послідовності можна без спотворень виділити передане повідомлення. Спектр дискретизованого за часом повідомлення показаний на Рис. 11.18. Як видно з рисунку, умова неспотвореного відновлення спектра повідомлення, тобто можливість виділення однієї із смуг, що містять повідомлення, саме та, що була проаналізована у попередньому розділі – це умова неперетинання цих смуг частот, тобто
функції (див. вираз (10.20)). Теорема визначає умови, за яких з прийнятої споживачем модульованої імпульсної послідовності можна без спотворень виділити передане повідомлення. Спектр дискретизованого за часом повідомлення показаний на Рис. 11.18. Як видно з рисунку, умова неспотвореного відновлення спектра повідомлення, тобто можливість виділення однієї із смуг, що містять повідомлення, саме та, що була проаналізована у попередньому розділі – це умова неперетинання цих смуг частот, тобто 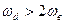 .
.
11.8. Підсумки та самоконтроль
Розділ присвячений вивченню можливостей багатоканального передавання та приймання повідомлень. Розглянуто дві можливості ущільнення (розділення) каналів зв’язку – частотна - коли повідомлення переноситься на фіксовану носійну частоту, та часова - коли у визначені моменти часу передаються окремі миттєві значення повідомлення. Обидві можливості реалізуються за допомогою модуляції - процесу зміни параметрів носійного коливання за законом повідомлення, що передається. У першому випадку носійним коливанням є синусне коливання, що відповідає умові 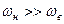 , у другому випадку носієм є періодична послідовність імпульсів, що відповідає умові
, у другому випадку носієм є періодична послідовність імпульсів, що відповідає умові 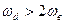 .
.
Повідомлення може носити неперервний(аналоговий) або дискретний характер, відповідно, розрізняють аналогову модуляцію та маніпуляцію носійного коливання. Спектр модульованого коливання завжди ширше спектра повідомлення (за винятком ОБС коливання).
Із розділу слід засвоїти визначення: носійна частота, модулювальна частота, частота (період) дискретизації, девіація частоти, глибина амплітудної модуляції, індекс кутової модуляції.
Поглибити знання за тематикою цього розділу можна, скориставшись літературою [2, p. 11], [3, гл. 13], [5, гл. 15, 20].
Проконтролювати засвоєння матеріалу цього розділу можна, відповівши на такі питання:
- Що таке коефіцієнт широкосмуговості сигналу?
- За яким параметром принципово відрізняються інформаційні та радіосигнали?
- У чому полягає процес модуляції?
- Яке співвідношення між частотами носійних та інформаційних коливань?
- Які види модуляції ви знаєте?
- Які основні властивості АМ коливань?
- Як позбутися надлишковості двосмугового АМ коливання?
- У чому полягає різниця між ФМ та ЧМ коливаннями?
- За яким параметром розрізняється «повільна» та «швидка» ЧМ?
- Яка різниця між телеграфними сигналами з пасивною та активною паузами?
- У чому полягає зміст дискретизації аналогового коливання?
- Яка мета дискретизації аналогового коливання?
- У чому полягає зміст теореми Котельникова?
- Яка умова відновлення без спотворень дискретизованого коливання?
- Що таке шум дискретизації?
12. АНАЛІЗ ПРОХОДЖЕННЯ СИГНАЛІВ ЧЕРЕЗ РАДІОЕЛЕКТРОННІ КОЛА
12.1. Характеристики сигналів та кіл
У будь-якому каналі зв’язку передавання повідомлення повинно відбуватися так, щоб інформація, що міститься у ньому не набула суттєвих змін, тобто не була зруйнована. Канал зв’язку складається з лінійних та нелінійних пристроїв, які тим, чи іншим чином змінюють повідомлення.
Метою аналізу проходження сигналів через пристрої є виявлення змін, що відбуваються з формою повідомлень на виході пристроїв. Зміни можуть бути запланованими з метою надання сигналу необхідної форми (наприклад, модуляція), або незалежними від розробника апаратури і додаючими спотворення до сигналів (наприклад, шуми або частотні спотворення).
Для визначення реакції пристрою на дію того чи іншого сигналу слід знати характеристики сигналу та характеристики пристрою.
Сигнал (коливання) можна описати:
1. у вигляді часової залежності миттєвих значень 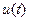 ;
;
2. у вигляді комплексного частотного спектра 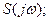
3. у вигляді операторного зображення 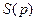 (див. у подальшому розгляді);
(див. у подальшому розгляді);
4. у вигляді автокореляційної функції 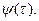
Лінійні кола можна описати:
1. передавальними функціями у частотній та операторній областях 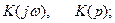
2. реакцією кола на випробувальні сигнали відомої форми 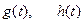 (далі буде).
(далі буде).
Нелінійні кола можна описати:
1. ВАХ для низьких частот дії;
2. залежністю ВАХ від частоти для широкого частотного діапазону дій.
Суттєвим є те, що для аналізу реакції пристрою на ту, чи іншу дію, слід мати опис і пристрою, і дії у однаковій системі координат – часовій, частотній або операторній. Тому завжди аналіз розпочинається з узгодження описів пристрою та вхідної дії.
12.2. Аналіз проходження коливань через лінійні пристрої
Аналіз впливу лінійного пристрою на сигнал ґрунтується на основній властивості лінійного кола, що реакція на суму дій дорівнює сумі реакцій на кожну дію окремо. Це надає можливість застосувати розклад сигналу на складові, на які відома реакція кола.
12.2.1. Спектральний метод аналізу проходження сигналів
Під час спектрального аналізу вхідну дію подають у вигляді спектра Фур’є
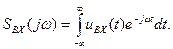 (12.1)
(12.1)
Коло описується частотною характеристикою коефіцієнту передавання
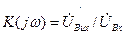 , (12.2)
, (12.2)
де вхідна і вихідна напруги є синусоїдами. Відповідно
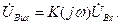 (12.3)
(12.3)
У разі дії складної форми
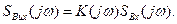 (12.4)
(12.4)
Тобто вплив кола на вхідну напругу полягає у тому, що кожна складова вхідної напруги набуває зміни амплітуди та фази у відповідності з параметрами коефіцієнту передавання кола на частоті складової. Форма вихідного коливання визначається за допомогою оберненого перетворення Фур’є
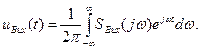 (12.5)
(12.5)
 Зміну форми сигналів у лінійних колах можна пояснити їхньою фільтрувальною властивістю, пов’язаною з наявністю у колі залежних від частоти реактивних опорів. Такі інерційні кола по різному передають частотні складові сигналу, що призводить до зміни його форми. Така властивість може бути небажаною і розцінюється як внесення у сигнал лінійних або частотних спотворень. Знайдемо умови неспотвореного передавання сигналу. Проходження сигналу через будь-який реальний пристрій відбувається за певний час, тому сигнал на виході пристрою завжди запізнюється відносно вхідного. Виходячи з цього, будемо вважати сигнал не спотвореним, якщо
Зміну форми сигналів у лінійних колах можна пояснити їхньою фільтрувальною властивістю, пов’язаною з наявністю у колі залежних від частоти реактивних опорів. Такі інерційні кола по різному передають частотні складові сигналу, що призводить до зміни його форми. Така властивість може бути небажаною і розцінюється як внесення у сигнал лінійних або частотних спотворень. Знайдемо умови неспотвореного передавання сигналу. Проходження сигналу через будь-який реальний пристрій відбувається за певний час, тому сигнал на виході пристрою завжди запізнюється відносно вхідного. Виходячи з цього, будемо вважати сигнал не спотвореним, якщо
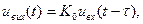 (12.6)
(12.6)
де 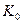 - коефіцієнт передавання кола,
- коефіцієнт передавання кола, 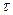 - час поширення сигналу з входу на вихід. Виходячи з властивостей спектрів, спектр вихідного сигналу у цьому випадку дорівнює
- час поширення сигналу з входу на вихід. Виходячи з властивостей спектрів, спектр вихідного сигналу у цьому випадку дорівнює
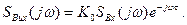
Звідки коефіцієнт передавання кола, що не додає спотворень буде
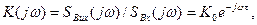 (12.7)
(12.7)
або 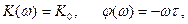 (12.8)
(12.8)
тобто вираз (8) описує АЧХ та ФЧХ кола, що не додає спотворень до сигналу. Ці характеристики кола подані на Рис. 12.1. Отже відсутність спотворень забезпечується рівномірною АЧХ та лінійною ФЧХ у всьому діапазоні частот сигналу. При цьому ФЧХ має крутість  яка дорівнює часові затримки сигналу у колі. Реальні кола мають обмежені смуги прозорості, отже не задовольняють умовам неспотвореного передавання. Однак, реальні сигнали теж мають спектри, обмежені за частотою. Ця обставина дозволяє спростити умови неспотвореного передавання реальних сигналів реальними колами, задаючи параметри кола у смузі, яку займає сигнал.
яка дорівнює часові затримки сигналу у колі. Реальні кола мають обмежені смуги прозорості, отже не задовольняють умовам неспотвореного передавання. Однак, реальні сигнали теж мають спектри, обмежені за частотою. Ця обставина дозволяє спростити умови неспотвореного передавання реальних сигналів реальними колами, задаючи параметри кола у смузі, яку займає сигнал.
Наприклад, проаналізуємо проходження АМ коливання через коливальний контур, що має коефіцієнт передавання  .
.
Спектр АМ коливання
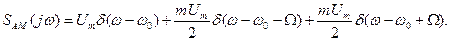
Підставимо ці вирази у співвідношення (4)
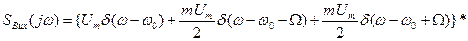
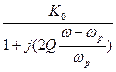 ,
,
тобто вихідний спектр має складові тих же частот (бо коло лінійне), амплітуда і фаза яких залежить від коефіцієнту передавання контуру на цих частотах. Можливі два випадки налаштування контуру:
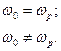
У першому випадку обидві бічні складові однаково зменшуються у  разів, тобто таким же чином зменшується m – глибина модуляції. У разі реального повідомлення, коли коливання містить багато складових спектра, вони зменшуються нерівномірно, в залежності від їх частоти, причому більше згасають високочастотні складові, які визначають «тонку» структуру повідомлення. У випадку нерівності носійної частоти та резонансної частоти контуру згасання бічних складових відбувається неоднаково і окрім амплітудних спотворень коливання набуває паразитної фазової модуляції, що може призвести до додаткових спотворень під час відтворення сигналу у приймачі.
разів, тобто таким же чином зменшується m – глибина модуляції. У разі реального повідомлення, коли коливання містить багато складових спектра, вони зменшуються нерівномірно, в залежності від їх частоти, причому більше згасають високочастотні складові, які визначають «тонку» структуру повідомлення. У випадку нерівності носійної частоти та резонансної частоти контуру згасання бічних складових відбувається неоднаково і окрім амплітудних спотворень коливання набуває паразитної фазової модуляції, що може призвести до додаткових спотворень під час відтворення сигналу у приймачі.
Читайте також:
- I. ОБРАЗОВАНИЕ СОЕДИНЕННЫХ ШТАТОВ 14 страница
- А. В. Дудник 1 страница
- А. В. Дудник 10 страница
- А. В. Дудник 11 страница
- А. В. Дудник 12 страница
- А. В. Дудник 2 страница
- А. В. Дудник 3 страница
- А. В. Дудник 4 страница
- А. В. Дудник 5 страница
- А. В. Дудник 6 страница
- А. В. Дудник 7 страница
- А. В. Дудник 8 страница
| <== попередня сторінка | | | наступна сторінка ==> |
| Приклад 2 4 страница | | | Приклад 2 6 страница |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |