Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Приклад 2 6 страница

Наведемо ще приклади спектрального аналізу радіоелектронних кіл. У радіоелектроніці часто є необхідність у перетворенні коливання, яке має характер диференціювання або інтегрування, тобто

або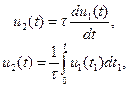

де 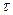- стала величина, що має розмірність часу. Для визначення схеми кіл, що можуть перетворити коливання таким чином, простіше скористатись спектральними співвідношеннями.

Спектр диференційованого коливання дорівнює

, (12.9)

а спектр інтегрованого коливання дорівнює

. (12.10)

Виходячи з виразу (4), диференціювальне коло повинно мати коефіцієнт передавання

, (12.11)

а інтегрувальне, відповідно,

. (12.12)

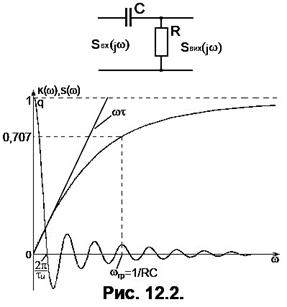
Кола з коефіцієнтами передавання, що прямують до нескінченності, реально створити не можна. Реальні кола виконують ці операції тільки наближено і тим точніше, чим у меншій смузі частот зосереджено спектр коливання. Розглянемо, наприклад, RC-коло, схему якого подано у верхній частині Рис. 12.2. Коефіцієнт передавання напруги кола дорівнює

(12.13)

де За умови вираз (13) наближається до (11), тобто коло виконує операцію диференціювання імпульсних коливань, у яких тривалість

У нижній частині Рис. 12.2 подано для порівняння АЧХ кола та спектр прямокутного імпульсу, тривалість, якого наближається до наведеної вимоги. На тому ж графіку накреслено дотичну до АЧХ пряму, яка, власне, і є АЧХ ідеального диференціатора. З рисунку видно, що умови більш менш точного диференціювання виконуються для перших двох пелюсток спектра імпульсу, де зосереджено приблизно 95% енергії імпульсу.

Для RC-кола, схему якого подано у верхній частині Рис. 12.3, коефіцієнт передавання напруги дорівнює

(12.14)

за умови вираз (14) наближається до (10), тобто коло виконує інтегрування імпульсних коливань, тривалість яких

У нижній частині Рис. 12.3 подано для порівняння АЧХ кола та спектр прямокутного імпульсу, тривалість, якого наближається до наведеної вимоги. На тому ж графіку накреслено гіперболу 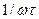, яка, власне, і є АЧХ ідеального інтегратора. З рисунку видно, що умови більш менш точного інтегрування виконуються вище граничної частоти кола.

Як видно з наведених прикладів, спектральним аналізом зручно користуватись, коли можна обмежитись розглядом спектру вихідного коливання, не вдаючись до аналізу його змін у часі. Ширшому застосуванню спектрального аналізу у тригонометричному базисі заважають такі недоліки перетворення Фур’є:

- базисними функціями розкладу є нескінченні періодичні функції (синуси і косинуси), що не дає змоги враховувати під час аналізу початкові умові, тобто початковий запас енергії у колі (напруги на ємностях, струми у індуктивностях, що є до початку дії), тобто аналізу підлягають тільки так звані «пусті» кола;

- розкладу Фур’є підлягають функції, що відповідають умовам абсолютної інтегрованості, які не завжди виконуються, особливо у разі моделювання;

- складно виконати обернене перетворення Фур’є навіть для найпростіших коливань.

12.2.2. Операторний метод аналізу проходження сигналів

Операторний метод є узагальненням спектрального методу аналізу проходження сигналів через кола, дозволяє уникнути усіх наведених вище недоліків перетворення Фур’є і тому широко застосовується у багатьох галузях аналізу процесів у лінійних системах.

Щоб позбутися першого недоліку перетворення Фур’є, введемо умову

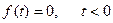. (12.15)

Подальшим узагальненням перетворення Фур’є є введення у якості базисної функції комплексної експоненційної функції 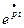, де 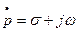, невдало назване комплексною частотою. Підсумовуючи два комплексних коливання за правилом одержимо дійсне коливання

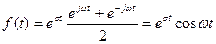. (12.16)

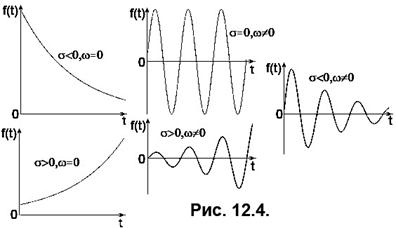Функція 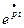є ортогональною функцією. В залежності від значень 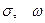можна одержати різноманітні дійсні коливання, подані на Рис. 12.4.

Найбільш «природним» випадком є 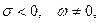що описує коливальні процеси у реальних колах з втратами. Тому за допомогою рядів ортогональних функцій виду 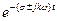можна подавати коливання, що відповідають умові 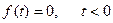. Таке подання називається перетворенням Лапласа, а метод аналізу кіл та коливань на основі перетворень Лапласа – операторним методом. Пряме перетворення Лапласа має вигляд

. (12.17)

За умови воно переходить у однобічне перетворення Фур’є. f(t) називається оригіналом, а F(p) – зображенням за Лапласом або просто зображенням. Наявність множника знімає проблему абсолютної збіжності f(t), тобто перетворення Лапласа можна застосовувати для подання, практично, будь-яких функцій. Обернене перетворення має вигляд

(12.18)

Властивості перетворень Лапласа та Фур’є, в основному збігаються, за винятком зображення диференційованої та інтегрованої функцій, а саме:

якщо 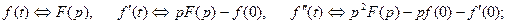(12.19)

якщо 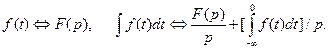(12.20)

На практиці широко використовують таблиці перетворень Лапласа, де подані співвідношення між оригіналами та зображеннями для багатьох функцій. У Таблиці 12.1 наведено відповідності між оригіналами та зображеннями найбільш поширених коливань.

Таблиця 12.1.

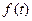
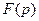
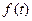
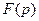
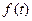
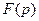
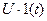
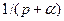
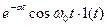
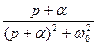
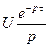
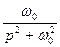
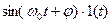
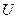
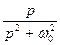
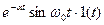
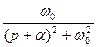
Опис характеристик кіл операторним методом виконується за умови 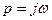, тобто у стаціонарному режимі. Відповідно, маємо зображення опорів

та коефіцієнту передавання тощо.

Застосуємо операторний метод для розрахунку нестаціонарного процесу у лінійному електричному колі, поданому у лівій частині Рис. 12.5. Запишемо закон Кірхгофа для кола

(12.21)

Застосуємо перетворення Лапласа до обох частин рівняння (21). У відповідності з виразами (19) та (20)

Підставимо ці вирази у (21) і одержимо рівняння Кірхгофа у операторній формі з урахуванням початкових умов, тобто струмів і напруг, що мали місце на початку розгляду процесу. Такої можливості урахування енергії, накопиченої у елементах кола до початку перехідного процесу, під час аналізу за Фур’є не було.

(12.22)

Одержане рівняння є лінійним алгебраїчним рівнянням з невідомою функцією . Схема кола, що описується операторним рівнянням (22) подана на Рис. 12.5, праворуч. Величини 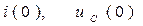подають початкові значення струму у колі і напруги на ємності. Ці величини можуть бути додатними або від’ємними, в залежності від умовно обраних додатних напрямків 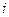та 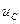. Таким чином, операторне рівняння автоматично враховує початкові умови, що описують вихідний енергетичний стан кола. Зображення струму у колі

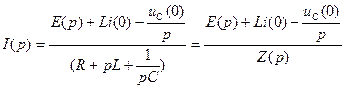. (12.23)

Якщо початковий запас енергії у колі дорівнює нулю, тобто 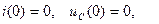вираз (23) спрощується

(12.24)

Рівність (24) за своїм видом співпадає із співвідношенням, що описує синусоїдне коливання у колі в усталеному режимі. За цією аналогією величину 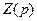називають операторним опором кола. Фізичне пояснення схеми у правій частині Рис. 12.5 полягає у тому, що індуктивність з початковим струмом є еквівалентною послідовному з’єднанню тієї ж індуктивності без початкового струму та додаткового джерела напруги . Відповідно, ємність, заряджена до початкової напруги , є еквівалентною послідовному з’єднанню тієї ж ємності без початкового заряду та додаткового джерела напруги.

Аналіз проходження коливання через коло операторним методом виконується у наступній послідовності:

- за електричною схемою визначається зображення коефіцієнта передавання кола ;

- прямим перетворенням Лапласа визначається зображення вхідного коливання ;

- за формулою визначається зображення вихідного коливання;

- оберненим перетворенням Лапласа визначається оригінал коливання на виході кола .

Скористаємось наведеним порядком аналізу для розрахунку реакції лінійного кола, поданого на Рис. 12.6, на одиничний стрибок напруги. Реакція лінійного кола на одиничний стрибок напруги або струму називається перехідною характеристикою кола 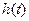. Розмірність перехідної характеристики збігається з розмірністю дії.

Операторний коефіцієнт передавання кола дорівнює

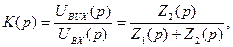(12.25)

де

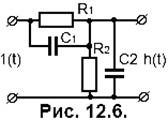Підставимо вирази операторних опорів ланок у формулу (25) і після перетворень одержимо

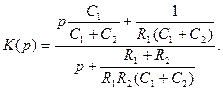(12.26)

Зображення вихідної напруги кола дорівнює

. (12.27)

Подальший перехід до часової форми реакції кола можна виконати або за допомогою таблиць (див. Таблицю 12.1), або скориставшись теоремою розкладення операційного числення. Мета теореми розкладення – подання зображення реакції у вигляді суми зображень, що відповідають оригіналам найпоширеніших форм коливань. Перетворимо вираз (27) саме таким чином

де - другий корінь знаменника виразу (27).

Скориставшись Таблицею 1 та властивостями перетворення Лапласа, одержимо часову функцію реакції кола на одиничний стрибок, тобто перехідну характеристику кола

. (12.28)

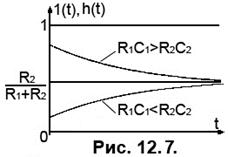
Вид функції (28) залежить від співвідношення опорів та ємностей кола. Можливі три варіанти співвідношення:

або

Часові діаграми для цих випадків подані на Рис. 12.7. Як видно з рисунку, у третьому варіанті вихідна напруга кола дорівнює

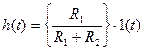, (12.29)

тобто коло не спотворює форму коливання, незалежно від наявності у ньому реактивних елементів. Коло, схему якого подано на Рис. 12.6, за умови 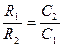, називається частотно компенсованим подільником напруги і широко використовується у вхідних і вихідних колах радіовимірювальних пристроїв. Частотна компенсація подільників напруги (ступінчастих атенюаторів) є необхідною, бо будь-які кола містять паразитні ємності, підімкнені паралельно до навантажувальних опорів ( у нашому випадку це 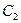та ). У підсумку подільник вносить частотні (і, відповідно, часові) спотворення, тобто змінює форму вхідних сигналів, що підлягають регулюванню. Єдиним способом уникнути цих спотворень є підбір компенсувальної ємності (у нашому випадку ) для досягнення співвідношення (29).

12.2.3. Часовий метод аналізу проходження сигналів

Крім перетворень Фур’є і Лапласа, коливання, що діє на вході кола можна подати у вигляді суми елементарних несинусоїдних дій, наприклад стрибків або прямокутних імпульсів, як показано на Рис. 12. 8,а,б. Елементарний стрибок функції у момент 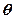дорівнює

За умови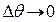

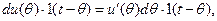(12.30)

інтегруючи елементарні стрибки за всією областю існування 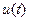, одержимо

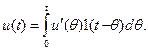(12.31)

Таким чином, щоб визначити реакцію лінійного кола на довільну дію, слід знайти його реакцію на дію у вигляді одиничного стрибка, а далі підсумувати ці реакції для усіх стрибків, з яких складається функція дії у відповідності до виразу (31).

Тобто, дії 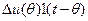відповідає реакція або, за умови 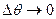, - . Відповідно, напруга на виході кола, для довільної дії на вході, дорівнює

(12.32)

Якщо вхідна дія має на початку стрибок скінченої величини (див. Рис. 12.9), то

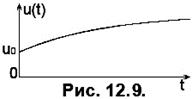
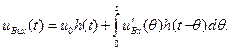(12.33)

Вираз (33) називається першою формоюінтегралу Дюамеля. Перехідна характеристика кола найчастіше визначається операторним методом. Визначимо, наприклад, перехідну характеристику RC-кола, схему якого подано на Рис. 12.2. Операторний коефіцієнт передавання напруги кола дорівнює

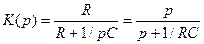зображення одиничного стрибка . Відповідно, зображення перехідної характеристики має вигляд

За Таблицею 1 знаходимо перехідну характеристику кола

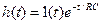Скористаємось одержаним результатом для визначення реакції кола на лінійну (пилкоподібну) напругу на вході

Підставляємо похідну від вхідної напруги та перехідну характеристику кола у вираз (33)

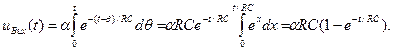
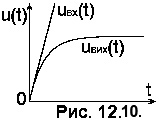Як бачимо з часової діаграми, поданої на Рис. 12.10, при значеннях часу 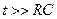, вихідна напруга кола прямує до сталої величини , пропорційної похідній від вхідної напруги, тобто коло є наближеним диференціатором.

У випадку подання вхідної дії у вигляді суми прямокутних імпульсів, що прилягають один до одного (див. Рис. 12.5,б), як і попередньому випадку, слід виконати умову 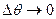, тобто подати коливання у вигляді сукупності зсунутих за часом 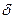-імпульсів, площа яких дорівнює миттєвим значенням дії

. (12.34)

Реакцію лінійного кола на дію, подану виразом (34), можна визначити, підсумовуючи реакції на 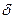- імпульси відповідних площ.

Реакція кола на 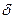-імпульс називається імпульсною характеристикою кола . Відповідно, відгук кола на 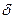- імпульс площі в момент 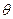дорівнює

а реакція на всю дію має вигляд

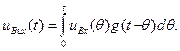(12.35)

Це друга формаінтегралу Дюамеля.

Враховуючи, що одержуємо зв’язок між імпульсною та перехідною характеристиками кола

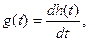(12.36)

тобто розмірність імпульсної характеристики співпадає з розмірністю похідної від дії.

Наприклад, Рис. 12.11 відображає перехідну та імпульсну характеристики наближеного диференціатора, розглянутого у попередньому прикладі, схему якого подано на Рис. 12.2.

Підставляючи у вираз (36) перехідну характеристику

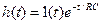одержимо

З спектральної точки зору, якщо на вході кола з коефіцієнтом передавання 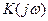діє 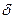- імпульс із сталою спектральною густиною на всіх частотах , спектр вихідного коливання

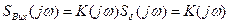
просто повторює частотну характеристику кола. Звідки імпульсна характеристика кола дорівнює

(12.37)

тобто імпульсна характеристика та коефіцієнт передавання кола зв’язані перетвореннями Фур’є

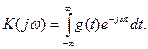(12.38)

Частіше використовують перетворення Лапласа

(12.39)

Аналіз проходження коливань різноманітної форми через лінійні кола дає змогу зробити висновок про вплив лінійного кола на коливання, який зводиться до зміни амплітуд і фаз його складових, або, що є еквівалентним, до зміни форми окремих елементів або коливання в цілому. Складових з новими частотами при цьому не виникає. Однак, для одночасного передавання багатьох повідомлень, сигнали слід розмістити на різних частотах або брати відліки їх миттєвих значень у різні моменти часу. А для цього необхідно утворювати нові складові з частотами, яких не було у вхідному коливанні (див. Розд. 11). Виконання такого завдання можливе тільки з використанням нелінійних кіл у поєднанні з фільтрувальними лінійними колами.

12.3. Перетворення спектра коливань у нелінійних колах

Принциповою відмінністю нелінійного кола від лінійного є виникнення на виході кола нових спектральних складових, яких не було у коливанні на його вході. Форма коливань на вході кола залежить від функції, яку коло виконує у конкретному пристрої. Коливання будь-яких форм, можна описати одним з трьох способів:

- як синусоїду (косинусоїду)

(12.40)

- як суму гармонік

(12.41)

- як суму негармонічних складових

(12.42)

Аналіз змін, які вносить нелінійне коло у вхідне коливання залежить від подання характеристики передавання кола та від діапазону зміни миттєвих значень коливання. У Розділі 9 було розглянуто кусково-лінійну та поліноміальну апроксимацію ВАХ нелінійного елементу. У першому наближенні робота пристрою розглядається у двох режимах:

- у режимі «малого» сигналу, коли використовується лінійна апроксимація ділянки ВАХ, на якій відбуваються зміни миттєвих значень вхідного та вихідного коливань. У цьому режимі пристрій розглядається як лінійний неінерційний прохідний чотириполюсник, який не змінює форму коливання. Метою аналізу є визначення його вхідного та вихідного опорів, а також коефіцієнтів передавання;

- у режимі «великого» сигналу, коли коливання охоплює значну частину ВАХ нелінійного елементу. У цьому випадку найчастіше використовується лінійна апроксимація окремих ділянок, які відрізняються нахилом апроксимувальних прямих. Режим використовується для аналізу умов утворення нових корисних складових вихідного коливання.

12.3.1. Аналіз у режимі «малого» сигналу

Для оцінювання якості передавання інформації слід визначати кількісні відмінності між сигналами на вході та на виході пристрою, тобто оцінювати величини спотворень, що вносяться пристроєм за рахунок відхилення ВАХ від прямої. Для аналізу спотворень, які виникають за рахунок впливу нелінійного елементу кола використовується апроксимація ВАХ у околі робочої точки степеневим поліномом

, (12.43)

де член поліному визначає неспотворену частку вихідного сигналу, решта – внесені відмінності. Така форма подання є зручною, бо дає можливість наочної кількісної оцінки змін, внесених до вхідного сигналу

Спектр вихідного коливання можна знайти, скориставшись формулами кратних дуг

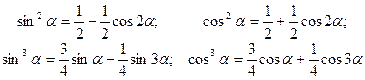тощо

та формулами добутків синусів і косинусів різних степенів, наприклад,

Підставимо вирази (40), (41), (42) у (43) і одержимо часові залежності струмів у нелінійному колі у разі дії різних за складністю напруг. Для косинусоїдної дії

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Приклад 2 5 страница	\|	Приклад 2 7 страница

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.012 сек.