
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Виникнення (походження) держави. 4 страница
2) Сила струму є похідна від функції, яка виражає залежність кількості електрики 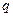 , яка протікає за час
, яка протікає за час 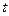 : якщо
: якщо  , то
, то  .
.
3) Кутова швидкість обертання тіла навколо осі є похідна від функції, яка виражає залежність кута повороту 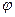 тіла відносно осі від часу
тіла відносно осі від часу 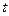 :
:
якщо 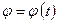 , то
, то  .
.
4) Лінійна густина матеріальної лінії в даній точці є похідна від функції, яка виражає залежність маси 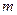 від довжини цієї лінії:
від довжини цієї лінії:
якщо 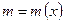 , то
, то 
5) Теплоємність тіла при даній температурі є похідна від функції, яка виражає залежність кількості тепла 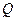 від температури
від температури 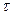 :
:
якщо  , то
, то 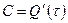 .
.
6) Швидкість хімічної реакції є похідною від функції, яка виражає залежність кількості речовини 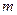 , яка вступила в реакцію від часу
, яка вступила в реакцію від часу 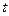 :
:
якщо 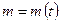 , то
, то 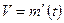
3. Геометричний зміст похідної.
Граничне положення січної 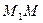 при прямуванні точки
при прямуванні точки 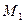 до точки
до точки 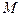
по кривій називають дотичною до кривої в точці М
Нехай крива, задана рівнянням 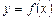 , має дотичну в точці М (х, у).
, має дотичну в точці М (х, у).
Геометричний зміст похідної функції в певній точці : похідна  чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х:
чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х: 
4. Рівняння дотичної і нормалі до плоскої кривої.
 Нехай функція у = f (t) означена і неперервна на деякому проміжку [a; b]..
Нехай функція у = f (t) означена і неперервна на деякому проміжку [a; b]..
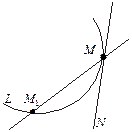
Рівняння дотичної:

де 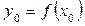 - значення функції в точці
- значення функції в точці 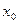
Нормаллю до графіка функції в точці М0 називається перпендикуляр, проведений до дотичної в цій точці.
Рівняння нормалі: 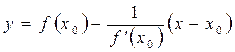
Приклад. Знайти рівняння дотичної та нормалі до графіка функції у = х2 у точці з абсцисою х0 = – 3.
1) знаходимо похідну від заданої функції 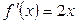 ;
;
2) знаходимо значення похідної в точці х0 = – 3:  ;
;
3) знаходимо значення функції в точці х0 = – 3:  .
.
4) рівняння дотичної запишеться так: 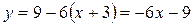
5) рівняння нормалі запишеться так: 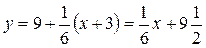
5. Основні правила диференціювання.
Якщо 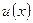 та
та 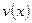 - деякі диференційовані функції, то
- деякі диференційовані функції, то
1) 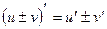
2) 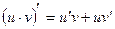
3) 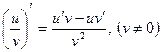
4) 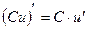
5) 
6. Таблиця похідних
1) 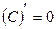
2) 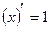
3) 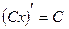
4) 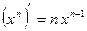
5) 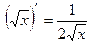
6) 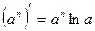
7) 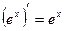
8) 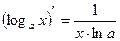
9) 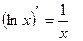
10) 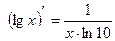
11) 
12) 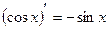
13) 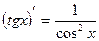
14) 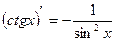
15) 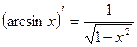
16) 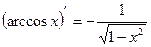
17) 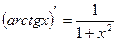
18) 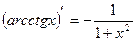
7. Похідна складної функції
1) 
2) 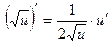
3) 
4) 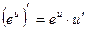
5) 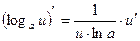
6) 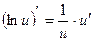
7) 
8) 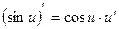
9) 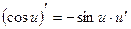
10) 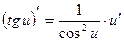
11) 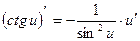
12) 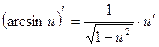
13) 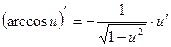
14) 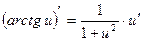
15) 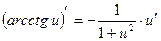
7. Загальна схема побудови графіків функцій:
1. Знайти область визначення функції.
2. Дослідити функцію на парність та непарність.
3. Визначити точки перетину з осями координат ( якщо це не викликає труднощів).
4. Знайти асимптоти графіка функцій:
Вертикальна асимптота:  х=а, за умови, що
х=а, за умови, що 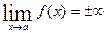
Похила асимптота  , де
, де 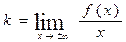 ,
, 
5. Знайти проміжки монотонності та точки екстремуму функції:
· Знайти похідну функції
· Прирівняти похідну до нуля та знайти можливі точки екстремуму функції( похідна в цих точках дорівнює нулю або не існує)
· Визначити знак похідної на кожному з проміжків: 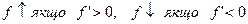
6. Знайти проміжки опуклості та точки перегину.
· Знайти другу похідну
· Прирівняти її до нуля та знайти точки перегину: .( похідна в цих точках дорівнює нулю або не існує)
· Визначити напрям опуклості: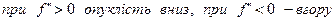
7. Побудувати графік функції, використовуючи результати дослідження.
8. Приклади для розв’язування
1. Знайти похідні функцій:
1) 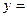

2) 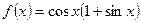
3) 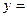

4) 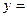
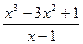
5) 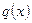

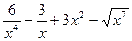
6) 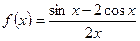
7) 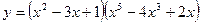
8) 
9) 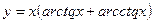
2.Розв’язати задачі:
1) Тіло рухається прямолінійно за законом 
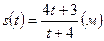 . Знайти швидкість тіла в момент
. Знайти швидкість тіла в момент 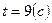 .
.
2) Дві матеріальні точки рухаються вздовж однієї прямої за законами 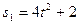
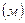 і
і 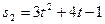
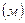 . знайти швидкості точок в ті моменти, коли пройдені ними відстані рівні.
. знайти швидкості точок в ті моменти, коли пройдені ними відстані рівні.
3.Обчислити значення похідних заданих функцій при вказаних значеннях незалежної змінної:
1) 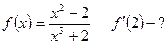
2) 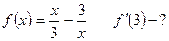
3) 
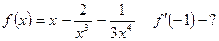
4) 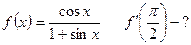
5) 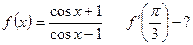
6) 
7) 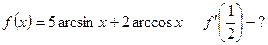
4.Розв’язати рівняння 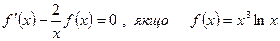
5.Розв’язати нерівність 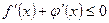
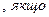
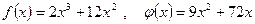
6.Розв’язати рівняння 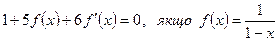
8. Скласти рівняння дотичної і нормалі до графіка функції 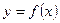 в точці
в точці 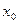 .
.
i. 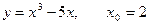
ii. 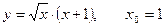
iii. 
iv. 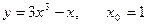
9. Під яким кутом до осі Ох нахилена дотична до графіка функції 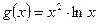 в точці з абсцисою 1?
в точці з абсцисою 1?
10. В яких точках дотична до кривої 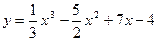 утворює з віссю Ох кут 450?
утворює з віссю Ох кут 450?
11. Знайти рівняння дотичної до графіка функції 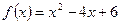 , яка паралельна прямій
, яка паралельна прямій 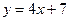 .
.
12. Скласти рівняння дотичних до кривих 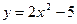 і
і 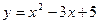 , які проходять через точки перетину цих прямих.
, які проходять через точки перетину цих прямих.
13. В яких точках дотична до графіка функції 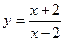 утворює з віссю Ох кут 1350?
утворює з віссю Ох кут 1350?
14. Знайти в якій точці графіка функції  дотична нахилена до осі абсцис під кутом
дотична нахилена до осі абсцис під кутом 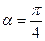 .
.
15. Знайти рівняння дотичної до графіка функції 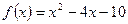 , яка паралельна прямій
, яка паралельна прямій 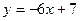 .
.
16.Знайдіть похідні функцій
1.  2.
2. 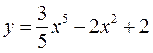
3. 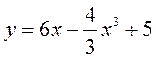 4.
4. 
5.  6.
6. 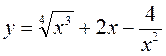
7. 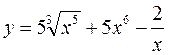 8.
8. 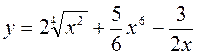
9.  10
10 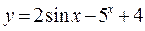 11.
11.  12.
12. 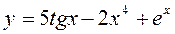 13.
13. 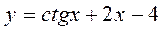 14.
14. 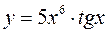 15.
15. 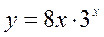 16.
16.  17.
17. 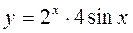 18.
18. 
19. *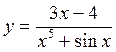 20. *
20. * 
21.* 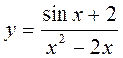 22. **
22. ** 
23.** 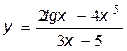 24. **
24. ** 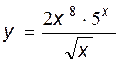
25.**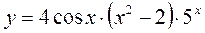 26. ***
26. *** 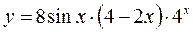
27. ** 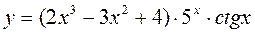 28 ***
28 *** 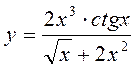
29. *** 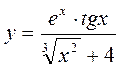 30. ***
30. *** 
17. **Знайдіть похідну складної функції.
1) 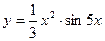
2) 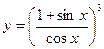
3) 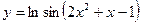
4) 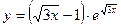
5) 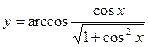
6) 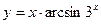
7) 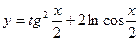
8) 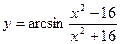
9) 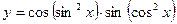
10) 
11) 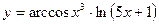
12) 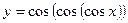
13) 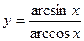
14) 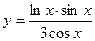
15) 
16) 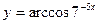
17) 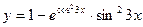
18) 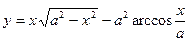
19) 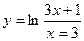
20) 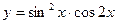
21) 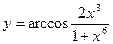
22)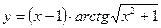
23) 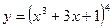
24) 
25)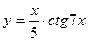
18.***Знайдіть похідні складних функцій
1.  2.
2. 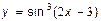
3.  4.
4. 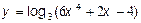
5.  6.
6. 
7. 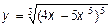 7.
7. 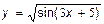
8. 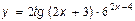 9.
9. 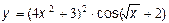
9.  10.
10. 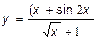
11. 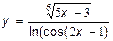 12.
12. 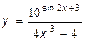
19.Дослідіть функцію на монотонність та екстремуми.
1. 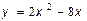 2.
2. 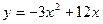
3. 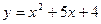 4.
4. 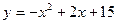
5. 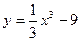 6.
6. 
7. 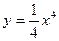 8.
8. 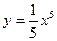
9. 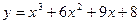 10.
10. 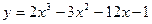
11. 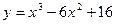 12.
12. 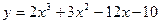
13. 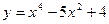 14.
14. 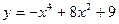
15. 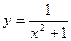 16.
16. 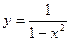
17. 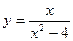 18.
18. 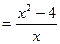
19.  20.
20. 
21. 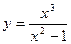 22.
22. 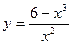
23. 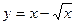 24.
24. 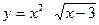
25. 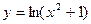 26.
26. 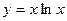
27.  28.
28. 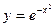
29. 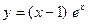 30.
30. 
31. 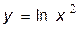 32.
32. 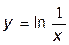
33. 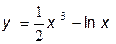 34.
34. 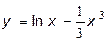
35. 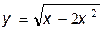 36.
36. 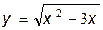
37. 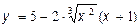 38.
38. 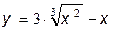
39. 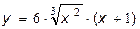 40.
40. 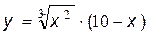
41. 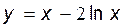 42.
42. 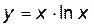
20.Знайдіть найбільше та найменше значення функції на проміжку
1. 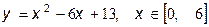 2.
2. 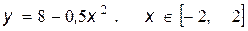
3. 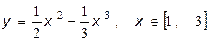 4.
4. 
5. 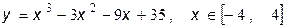
6. 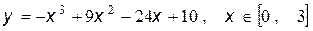
21. ***Задачі на знаходження найбільших та найменших значень величин.
1. Закон прямолінійного руху тіла заданий рівнянням S= - t3 +t2 +9t +3. Знайдіть максимальну швидкість руху тіла, якщо S задане в метрах, а t - в секундах.
2. Закон руху тіла, підкинутого вертикально вгору, заданий рівнянням
S = v0 t – 0,5g t2. Знайдіть найбільшу висоту підйому тіла.
3. Закон руху тіла, підкинутого вертикально вгору, заданий рівнянням
S = 19,6 t – 4,9 t2. Знайдіть найбільшу висоту підйому тіла, якщо S задане в метрах, а t - в секундах.
4. Закон деякого прямолінійного руху заданий рівнянням
S = 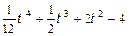
Знайдіть максимальне прискорення руху цього тіла, якщо S задане в метрах, а t - в секундах.
5. Які сторони повинен мати прямокутник, зігнутий з дротини довжиною 50 см, щоб його площа була найбільша?
6. Добуток двох додатніх чисел дорівнює 169. Якими повинні бути ці числа, щоб їх сума була найменшою?
7. З усіх прямокутників з периметром 40 см знайдіть той, у якого діагональ найменша.
8. В рівносторонній трикутник з периметром 90 см вписаний прямокутник найбільшої площі. Знайдіть довжини сторін цього прямокутника.
Розділ 6. ІНТЕГРАЛ ТА ЙОГО ВИКОРИСТАННЯ
1. Первісна та невизначений інтеграл.
2. Основні властивості невизначеного інтеграла.
3. Таблиця невизначених інтегралів.
Читайте також:
- I. ОБРАЗОВАНИЕ СОЕДИНЕННЫХ ШТАТОВ 14 страница
- XVII ст.). Виникнення козацтва.
- А. В. Дудник 1 страница
- А. В. Дудник 10 страница
- А. В. Дудник 11 страница
- А. В. Дудник 12 страница
- А. В. Дудник 2 страница
- А. В. Дудник 3 страница
- А. В. Дудник 4 страница
- А. В. Дудник 5 страница
- А. В. Дудник 6 страница
- А. В. Дудник 7 страница
| <== попередня сторінка | | | наступна сторінка ==> |
| Виникнення (походження) держави. 3 страница | | | Виникнення (походження) держави. 5 страница |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |